同値関係 | 類別というクラス分けをわかりやすく学習できる例を使いながら理論を解説
集合S上の二項関係～が、反射律・対称律・推移律を満たしているとき、" 同値関係 “といいます。
S上の同値関係が与えられると、互いに交わりが空集合となっている同値類たちにSを類別することができます。
大学の数学を学習するときに、様々な同値関係を扱います。
この記事では、xy-座標平面上の直線を使った同値関係の具体例を使っています。
わかりやすい例を通して、集合上の同値関係を用いて、類別をするということを解説します。
同値関係 :まずは二項関係の定義から
【二項関係の定義】
S を空でない集合とします。
a, b ∈ S について、組 (a, b) が特定の条件を満たすか、満たさないかを判定できるときに、S 上の二項関係といいます。
S 上の二項関係について、x, y ∈ S の組 (x, y) が、その特定の条件を満たすとき、x ～ y と表すことにします。
S の二つの元の組 (x, y) について、特定の条件を満たすかどうかを判断することができる二項の関係です。
二項関係の具体例を見てみます。
定義と照らし合わせることで、内容が理解できるかと思います。
S = {1, 2, 3, 4, 5} という集合上の二項関係の例です。
x, y ∈ S に対して、x を 3 で割ったときの余りと、y を 3 で割ったときの余りが等しいときに、x ～ y とします。
この ～ は、S 上の二項関係です。
次に、もう少し複雑な二項関係の例を述べます。
二項関係の具体例
空ではない集合として、xy 座標平面を考えます。
S = {(x, y) | x と y は実数} が座標平面を表す集合です。
この集合の元は、((x1, y1), (x2, y2)) という「組と組」の組になりますが、次のように考えるとスムーズに把握できるかと思います。
点 A (x1, y1)、点 B (x2, y2) となっていて、これら二つの座標について、特定の条件を満たすかどうかを判断するということだと考えます。
では、特定の条件として、「二つの点が、傾き 3 となっている同じ直線の上にある」とします。
この条件を満たすかどうかを判断するのは、一つの直線を表す一次関数の式に代入して判断します。
二つの点の座標で調べて、条件を満たすときに「～（チルダー）」の印で表します。
(0, 2) と (2, 8) について判断をしてみます。
y = 3x + 2 という直線の上にどちらの点もあることが分かります。
点 (0, 2) が、この直線の上にあることは、x に 0 を代入し、y に 2 を代入すると等式になることから分かります。
点 (2, 8) についても同様に考えます。
2 = 3 × 0 + 2,
8 = 3 × 2 + 2
これで、どちらも同じ傾き 3 の直線上の点なので、(0, 2) ～ (2, 8)
今度は、(0, 2) と (2, 9) について判定をします。
9 = 3 × 2 + 3 より、
点 (2, 9) は直線 y = 3x + 3 の上にあります。
点 (0, 2) は、違う直線 y = 3x + 2 の上にありました。同じ直線の上にあるという条件を満たさないので、「～」ではありません。
ここから、同値関係について解説します。
同値関係 :三つの条件を満たすとき
【同値関係の定義】
空でない集合 S 上の二項関係 ～ が次の三つの条件を満たすときに、同値関係といいます。
■ 反射律
a ∈ S に対して、a ～ a
■ 対称律
a ∈ S に対して、a ～ b ならば b ～ a
■ 推移律
a, b, c ∈ S に対して、
a ～ b かつ b ～ c ならば a ～ c
上で述べた二項関係が、「反射律、対称律、推移律」の三つの条件をすべて満たしているときに、同値関係といいます。
そのため、同値関係とは、二項関係の特別なものになります。
先ほどの「同じ傾き 3 の直線上にある」という二項関係は、同値関係になっています。同値関係の定義を満たしているかどうかを確認します。
定義を確認
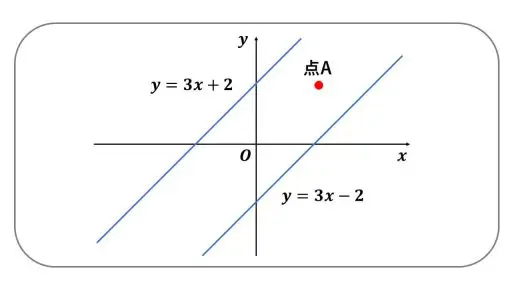
反射律から確認します。点 A (p, q) を xy 座標平面上の点とします。
傾き 3 の直線の切片をいろいろと変えると、ある値の切片のときに、点 A が直線の上に乗ります。
その直線を y = 3x + t とします。
点 A が、この直線の上にあるとき、当然、点 A が直線 y = 3x + t の上にあります。
ですので、(p, q) ～ (p, q) となっています。これで、反射律が確認できました。
次に対称律を確認します。
(p, q) ～ (r, s) を満たしていたというときに、ひっくり返しても「～」となっているかということの確認です。図形的にイメージすると分かります。
(p, q) ～ (r, s) より、これら 2 点が、どちらも同じ直線 y = 3x + c の上にあるということです。
このときに、点 (r, s) と点 (p, q) は、同一の直線 y = 3x + c にあります。
最後に推移律を確認します。
(p, q) ～ (r, s) かつ (r, s) ～ (v, w) となっているときに、(p, q) ～ (v, w) となっていることを示すことになります。これも、図形的にイメージすると分かりますが、念のために計算をして確認してみます。
(p, q) ～ (r, s) より、点 (p, q) と点 (r, s) が、傾き 3 の同じ直線 y = 3x + k の上にあります。
そして、(r, s) ～ (v, w) より、傾き 3 の同じ直線 y = 3x + h の上にあります。
ここで、点 (r, s) について、
s = 3r + k かつ s = 3r + h
よって、3r + k = 3r + h となっています。
3r は移項すると、消え、k = h となります。これで、どちらの切片も等しいことが分かりました。
そのため、y = 3x + k と y = 3x + h は、同じ傾き 3 の直線ということになります。したがって、点 (p, q) と 点 (v, w) が、傾き 3 の同じ直線の上にあるということになります。
よって、(p, q) ～ (v, w) が示せました。
同値関係とならない二項関係の例
ここまで、二項関係の特別なものが同値関係ということを述べてきました。
同値関係を理解するために、二項関係だけれど同値関係ではない例を見てみるのも良いかと思います。
なんでも同値関係というわけではないということを認識することで、同値関係への理解が深まるかと思います。
上で述べた二項関係とは別の例として実数の大小関係があります。実数全体 R 上の「小さい（大きい）」についての関係を表すのが不等式です。
a, b ∈ R について、「a が b より小さい実数」というのが特定の条件です。上で「～」で表していましたが、不等式の場合、「<」で表します。
3 は 5 より小さい実数なので、3 < 5 となります。
では、この左の実数が、右の実数よりも小さいという二項関係は同値関係でしょうか。その答えは、すぐに分かります。反射律の段階で、すぐに満たさないことが分かります。
3 < 3 は成立しません。また対称律も成立しません。
3 < 5 ですが、5 < 3 は成立しません。
ただし、推移律は成立して、よく使うので注意です。
同値関係ではない二項関係の例を述べました。次は、集合上の同値関係が与えられたときに、その集合を類別できるという集合論の内容です。
同値関係 :同値類 と商集合
空でない集合 S 上の同値関係 ～ が与えられているときに、同値類という S の特別な部分集合を考えます。
a ∈ S に対して、a を含む同値類を C(a) と表すことにします。
この a を含む C(a) という同値類の定義は、a と「～」となっている S の要素（元）をすべて集めたものです。
集合の記号で表すと、
C(a) = {x ∈ S | a ～ x} となります。
この同値類は、単なる部分集合と違って、次のことが必ず成立します。
「a, b ∈ S について、C(a) と C(b) が異なる集合であれば、必ず共通部分が空集合」になります。高校の数学で学習する背理法を使います。
C(a) ≠ C(b) だけど、C(a) ∩ C(b) が空集合ではないと仮定します。
すると、空でないので、C(a) ∩ C(b) に含まれている要素 t が存在します。
t ∈ C(a) ∩ C(b) ⊂ C(a) より、t ∈ C(a) です。
これは、同値類の定義から、a ～ t ということです。
任意の x ∈ C(a) について、a ～ x なので、対称律から、x ～ a です。
今、x ～ a かつ a ～ t より、推移律が成立するので、x ～ t となります。
t ∈ C(a) ∩ C(b) ⊂ C(b) なので、t ∈ C(b) でもあり、b ～ t です。
対称律から、t ～ b となっています。
今、x ～ t かつ t ～ b となっているので、推移律から、x ～ b となります。
よって、同値類の定義から、x ∈ C(b) となっています。
このため、C( a) は C(b) の部分集合となります。
さらに、任意の y ∈ C(b) に対して、b ～ y より、y ～ b です。
b ～ t も成立していたので、y ～ t となります。
t ～ a が成立していたので、y ～ a です。
つまり、a ～ y です。これは、同値類の定義から、y ∈ C(a) ということになります。
このように、C(a) が C(b) の部分集合であり、かつ、C(b) が C(a) の部分集合となるので、C(a) = C(b) となってしまいます。
しかし、これは C(a) ≠ C(b) であったことに矛盾します。
したがって、背理法から、C(a) ∩ C(b) が空集合であるということになります。
これで、異なる同値類どおしは、必ず共通部分が空集合になっているということが分かりました。
さらに、任意に a ∈ S をとってきたときに、必ず a を含む同値類が存在するということが分かります。これは、同値関係の反射律から導かれます。
a ～ a と必ずなるので、a ∈ C(a) ということで、a を含む同値類は必ず存在します。
このため、集合 S について、同値関係「～」についての同値類をすべてで和集合をとると、全体 S に必ず一致します。
任意の a ∈ S に対して、a ∈ C(a) が効いています。しかも、異なる同値類どおしの共通部分は空集合なので、同値類すべての和集合は、集合 S を分割していることになります。
S = ∪aC(a),
C(a) ≠ C(b) ならば C(a)∩C(b) = Φ
この同値類で集合 S を分割することを、同値類によって類別するといいます。
集合 S 上の同値関係が与えれられたとき、その同値類をすべて集めた集合たちの集まりを商集合といいます。
商集合という名前ですが、集合たちを集めた集合系のことです。
やはり具体例で確認
上で述べた「傾き 3 の同じ直線上にある」という同値関係「～」について、具体的に同値類を観察してみます。
先ほどの抽象的な証明は難しいので、この具体例を通して、じっくり同値類についての理解を深めると理解しやすいかと思います。
点 (0, 2) と「～」の関係になる点全体が、点 (0, 2) を含む同値類 C(0, 2) です。
図形的イメージから分かるように、この C(0, 2) は、直線 y = 3x + 2 上にある点をすべて集めた集合です。
xy 座標平面の部分集合となっています。特に、(－1, －1) や (－2, －4) は C(0, 2) に含まれています。
今、傾きが 3 の直線だけを考えていますので、切片を指定すると、それについての同値類が一つ定まる状況です。
先ほど、異なる同値類どおしの共通部分が空集合となることを抽象論で証明しました。具体例で見てみると、よく実感できます。
(0, 3) を含を含んでいる同値類 C(0, 3) は、直線 y = 3x + 3 上の点をすべて集めた集合です。
同値類 C(0, 2) は、直線 y = 3x + 2 上の点をすべて集めた集合なので、C(0, 3) との共通部分は空集合となっています。
一つの同値類は、傾き 3 の直線の切片によって一つ定まります。
そのため、切片として考えられるすべての実数について、それぞれの傾き 3 の直線に対応する同値類すべてで和集合をとると、xy 座標平面全体になります。
同値関係 ; 有限個の同値類の例
整数について、合同という二項関係は反射律・対称律・推移律を満たします。
ブログ7の倍数判定法より
S = {1, 2, 3, 4, 5} において、3 で割ったときの余りが等しいかどうかという二項関係 ～ は同値関係となっています。
※ 初等整数論で、この ～ を合同記号 ≡ を用いて表すことが多いです。
整数 a を含む同値類 C(a) を書き出してみます。整数を 3 で割ったときの余りは、0 か 1 か 2 なので、三個の同値類が得られます。
＜余りが 0 の同値類 C(0)＞
S の元で、3 で割ったときの余りが 0 となるのは、3 のみです。
そのため、C(0) = {3} です。
＜余りが 1 の同値類 C(1)＞
3 で割ったときの余りが 1 となる S の元は、1 と 4 です。
よって、C(1) = {1, 4}
＜余りが 2 の同値類 C(2)＞
S の元で、3 で割ると 2 余るものは、2 と 5 です。
C(0) ∪ C(1) ∪ C(2) が S になります。
S = {1, 2, 3, 4, 5}
= C(0) ∪ C(1) ∪ C(2)
= {3} ∪ {1, 4} ∪ {2, 5}
異なる同値類どおしの共通部分は空集合でした。確かに、3 つの同値類の和集合に分割されているということになります。
同値類についての学習をするときに、高校や中学では使わない用語や記号がハードルになるかもしれません。
しかし、すでに学習をした内容で、同値関係や同値類に類別することが使われています。
うまく具体例を使って、定義や一般的な証明と照らし合わせてみると、内容の理解が深まるかと思います。
小学生のときから知っている例
小学生の低学年から、同値関係を学習しています。
ある小学校の三年生が、100 名だとします。この三年生のクラスは、A 組と B 組と C 組だったとします。
この 100 名から成る集合を S として、「同じクラスの生徒」ということで二項関係を定めると同値関係になります。
A 組に属している生徒たちが、一つの同値類です。B 組も C 組も同様です。
どの二つの部分集合である組の共通部分も空集合です。和集合をとると、100 名からなる三年生全体の集合 S に一致します。
数学の記号を使って、記述をしてみます。
x, y ∈ S が同じクラスの生徒のとき、
x ～ y と定義する。
このように、定めます。
そして、A 組の生徒全員から成る集合を X と表すことにします。そして、B 組全員を Y, C 組全員を Z とします。
100 名の生徒全員の集合 S は、X ∪ Y ∪ Z という和集合と一致しています。
※共通部分 和集合 という記事で、高校で学習する和集合と共通部分について解説をしています。
今、A 組の生徒一人 a を固定します。このとき、a と「～」の関係になっている生徒を全員集めた S の部分集合を考えます。
つまり、a と同じクラスの生徒を全員集めてできる部分集合を考えます。
C(a) = {x ∈ S | a ～ x} と表します。
この部分集合に含まれる生徒は A 組の生徒全員なので、X と一致します。この部分集合が、a を含む同値類と数学の用語でいいます。
B 組の生徒は、誰も X には含まれていません。B 組の生徒である b ∈ Y を今度は一人固定します。
C(b) = {y ∈ S | y ～ b} です。
この部分集合は、b を含む同値類です。b は B 組の生徒なので、b と同じクラスの生徒を全員集めた部分集合なので、Y と一致します。
X ∪ Y に含まれていない生徒は、C 組の生徒です。c ∈ Z を一人、固定します。
C(c) = {z ∈ S | z ～ c} と表すと、Z と一致しています。
これで、S は、どの二つの部分集合も共通部分が空集合となっている部分集合たちの和集合として分割されました。
S = C(a) ∪ C(b) ∪ C(c)
C(a), C(b), C(c) のどの二つも共通部分が空集合となっています。
このように、集合において与えられた同値関係を使って分割をすることを類別といいます。
また、組合せの公式 nCr は、同値関係を用いることで導けます。
選んだ r 個の順列について r 個の順列を構成している文字を並び替えたときに、同じになる順列になっているときに ～ と定義すると類別できます。
これで今回の記事を終了します。
読んで頂き、ありがとうございました。