内心 – 外心 | 三角形に内接する円の中心をベクトル表示する【平面図形の定理を利用】
" 内心 – 外心 “を位置ベクトルで表示することを解説しています。
はじめに、三角形の３本の内角の二等分線が、ただ１点でのみ交わることを示します。
その後で、ベクトルの分点について、適切に公式を使うことで交わった１点である内心を位置ベクトルで表示します。
三角形の五心について、比較的に取り組みやすい内容になるので、平面図形の単元で学習した内容を思い出しつつ、ベクトルについての練習ができます。
この記事では、与えられた三角形ABC の外部に位置ベクトルの基準を取り、点 A(a) というように、位置ベクトルを小文字を使って表すことにします。
まずは内心について述べ、後で外心について解説します。
内心 :内部で交わる１点
三角形ABC が与えられたとします。
BC = p, CA = q, AB = r という辺の長さとします。
そして、∠A, ∠B, ∠C の二等分線が、それぞれの対辺と交わる点を D, E, F とします。
次の図のような状況になっています。
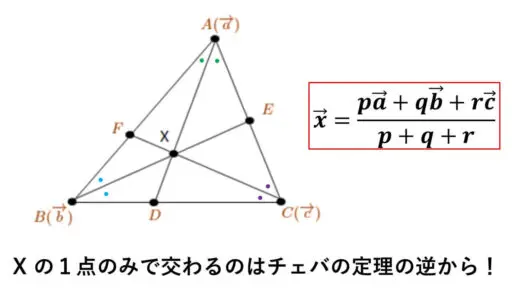
ここで、直線AD と直線BE は平行でないため、１点 X で交わります。
しかし、直線CF も点 X で他の二本の角の二等分線と交わるかどうかは、これだけでは不明です。
そこで、まずは直線CF も点 X を通るということを証明します。
つまり、三本の角の二等分線が、すべて点 X の１点のみで交わるということを証明します。
この内容が証明できると、この点 X が三角形ABC の内接円の中心ということになります。
点 X から、三角形の三辺に垂線を引くと、直角三角形の合同条件から、下した３本の垂線の長さが全て等しいことが分かり、点 X を中心とする円の半径だと分かるからです。
この中学の数学で学習した内容の前提となるのが、ただ１点 X のみで三本の角の二等分線が交わっているということになります。
ここから、中学の相似の単元で学習した有名な比の内容を使います。
角の二等分線と辺の交点と内分比
∠A の二等分線について、
BD : DC = AB : AC
= r : q となっています。
この中学の相似の単元で学習した内容ですが、高校の図形でも使います。
∠B についても、
CE : EA = BC : BA
= p : r となっています。
∠C に関しても、
AF : FB = CA : CB
= q : p です。
ここまでの内容を比の値の形でまとめます。
すると、高校一年の平面図形の単元で学習した有名な定理が使えることが分かります。
比の値をよく見る
今、
BD/DC = r/q,
CE/EA = p/r,
AF/FB = q/p となっています。
これら三つの等式を辺々掛け合わせます。
すると、
BD/DC・CE/EA・AF/FB
= r/q・p/r・q/p
= p/p・q/q・r/r
= 1・1・1 = 1 となります。
よって、チェバの定理の逆より、
直線AD, BE, CF は、ただ１点のみで交わることになります。
これで証明が完了しました。
※ 三角形の面積比という記事で、チェバの定理の逆の証明を解説しています。
ここまでは、高校一年の平面図形の内容でしたが、ここからはベクトルの内容も加えて議論を進めます。
点 X の位置ベクトル x を三角形の三つの頂点の位置ベクトルと三辺の長さを用いて表すことを目標として考えます。
内心 : 位置ベクトルで表示する
BD/DC = r/q,
CE/EA = p/r,
AF/FB = q/p と内分比が、辺の長さを用いた比で得られています。
この内容を、ベクトルの分点公式と合わせます。
点 X は線分AD の内分点です。
そして、点 D は線分BC の内分点です。
そのため、点 D を内分点の公式で位置ベクトル表示をし、線分AD にも内分点の公式を使うことで、点 X の位置ベクトル表示が得られるというわけです。
点 D が r : q に線分BC を内分していることを位置ベクトルを使って表示します。
d = 1/(r+q)(qb+rc) です。
与えられたのは三角形ABC の１つでしたが、今や三角形は他にもあります。
ここで、直線BE は三角形ABD における ∠B の二等分線にもなっています。
同様の議論をもう一度
直線BE と辺BD の交点 X について、中学の相似の単元で学習した内分比の式を使います。
AX : XB = AB : BD です。
点 D が r : q に線分BC を内分していることから、線分BD の長さを与えられた p, q, r という三辺の長さを使って表示することができます。
BD = r/(r+q) × BC
= pr/(p+r) です。
AB = r なので、
AX : XD
= r : pr/(r+q)
= (r+q) : p です。
これで、目標が補足できました。
点 X の線分AD の内分比が得られたので、内分比の公式が使えます。
点 D の位置ベクトル表示と合わせて、点 X の位置ベクトル表示を求めます。
位置ベクトル表示を完了
これで、点 X の位置ベクトル表示が完了しました。
ベクトルの内分点の公式を２回使い、スカラー倍の部分を正確に計算することで得られた式になります。
内心については、三本の角の二等分線ということから、中学の相似の単元で学習した辺の内分比の式が役立ちました。
これと似たような類推で、
BD : DC = p : q,
CE : EA = r : p,
AF : FB = q : r という状況から三角形の内部に交わる１点の位置ベクトルの表示を得ることができます。
この内容は、チェバの定理の逆という記事で解説をしています。
ここまで、ベクトルについての計算を扱ってきましたが、実数についての計算も大切になります。
実数の計算が役立つ例として、三角形の内接円について、三角形の面積と内接円の半径を結び付ける公式について説明をします。
内接円の半径
【面積】
三角形ABC について、
BC = a, CA = b, AB = c とする。
また、三角形ABC の内接円の半径を r とする。
ただし、a, b, c, r は定数で実数とする。
このとき、
△ABC = r/2 × (a+b+c) である。
＜証明＞
三角形ABC の内接円の中心を O と置きます。
３辺BC, CA, AC は、内接円に接しています。
そして、点 O と BC, CA, AC の距離は半径 r です。
さらに、△ABC の面積は、
△OBC, △OCA, △OAB の面積の和です。
ここで、△OBC, △OCA, △OAB の高さは r となっています。
そのため、
△OBC = a × r ÷ 2
= r/2 × a,
△OCA = r/2 × b,
△OAB = r/2 × c です。
ここまでの内容をまとめます。
実数についての計算
以上の内容より、
△ABC の面積は、
r/2 × a+ r/2 × b+ r/2 × c です。
ここで、実数についての計算なので、共通因数 r/2 でくくり出します。
因数分解をすると、
r/2 × a+ r/2 × b+ r/2 × c
= r/2 × (a+b+c) です。
すなわち、
△ABC = r/2 × (a+b+c) です。【証明完了】
ベクトルの和とスカラー倍に他に、通常の実数の計算規則も大切なので、日頃からトレーニングをしておくと良いかと思います。
ここからは、外心の位置ベクトル表示についての内容です。
外心 :位置ベクトルで表す
【命題】
三角形ABC と、その内部の点 X が与えられたとする。
そして、
△XBC : △XCA : △XAB
= p : q : r とする。
（ただし、p, q, r は正の実数）
さらに、AX と辺BC の交点を D、BX と辺CA の交点を E、CX と辺AB の交点を F とする。
このとき、点 X を位置ベクトル表示することができる。
まず、この命題の仮定の内容から、三角形の面積比と各辺の内分比の関連について述べておきます。
数学Aの平面図形の単元で学習する内容を使います。
辺AX を共通の底辺と考えると、
△XAB と△XCA の面積比は、
辺BD と辺DC の長さの比となります。
そのため、
BD/DC = △XAB/△XCA
= r/q となります。
これで、BD : DC = p : q で、点 D が辺BC を内分する比が分かりました。
当初は、この先の内容も述べていたのですが、
かなり長くなるので、
こちらの記事で続きを述べることにします。
【三角形の五心】
三角形の五心は、平面図形で学習する内容を復習しつつ、ベクトルの練習ができるので、位置ベクトルで表示することにチャレンジしておくと良い学習になるかと思います。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。
