2変数関数の連続性 | 具体的な関数でεとδを用いた定義に基づいて確認

" 2変数関数の連続性 “について、具体例を用いて、任意に与えられた正の実数 ε に対して、正の実数 δ が存在し、その δ-近傍内の任意の二点間の距離が ε 未満となることを確認します。
2変数関数についての連続性の定義を押さえつつ、多くの方が知っている二変数関数を使って、連続性の確認を行います。
抽象的な関数の基礎となる連続性の理論を、シンプルな例を通して眺めてみると、内容の理解の手助けとなるかもしれません。
高校の数学2で学習した円の内部についてのイメージが、連続性の判断の役に立ちます。
2変数関数の連続性 :よく知る具体例で
{(x, y) | x, y は実数} という集合が、xy-座標平面上(二次元ユークリッド空間)の点全体です。
実数全体を R と表すことにすると、
R2 = R×R という直積集合が、
R2 = {(x, y) | x, y は実数} となります。
f : R2 → R という関数(写像)が、定義域を二次元ユークリッド空間の点全体とする 2 変数の実数値関数です。
実は、この 2 変数の実数値関数の例を、算数や中学の数学で学習しています。
二つの実数を x, y とすると、
(x, y)∈R2 です。
この (x, y) について、x と y の乗法を計算した値である積 xy を対応させる関数(写像)を f とします。
f : R2 → R という 2 変数の実数値関数が定義できました。
f(x, y) = xy です。この f は代数学の入門を学習したときに出てくる R における乗法を表す写像(関数)です。
この記事では、この f が R2 を定義域とする連続関数であることを証明します。
まず、連続であることの定義を確認します。距離関数と近傍という円の内部を使った連続の定義です。
連続である定義
d : R2×R2 → R を、
((x, y), (u, w))∈R2×R2 に対して、
{(u-x)2+(w-y)2}1/2 と定義します。
(x, y), (u, w) という座標平面上の二点について、数学2で学習した三平方の定理を用いた二点間の距離を対応させるという関数が d という距離関数です。
この距離関数 d を使って、半径 δ の円の内部である δ-近傍が定義されます。
※ 3変数以上の距離関数の定義は、リンク先の記事で解説をしています。
この近傍を使って、2変数関数が連続であることが定義されます。
(a, b)∈R2 と 正の実数 δ が与えられたとき、
{(x, y)∈R2 | d((a, b), (x, y)) < δ} を
U((a, b), δ) と表します。
この U((a, b), δ) という R2 の部分集合は、
点 (a, b) を中心とする半径 δ の円の内部です。
次に、
f : R2 → R という 2変数関数が連続であることの定義です。
より一般的に、S ⊂ R2 を空ではない部分集合とし、S を定義域とする 2変数の実数値関数が連続であることを定義します。
f : S → R とします。
任意の正の実数 ε と任意の (a, b)∈S に対して、ある正の実数 δ が存在し、
「任意の (x, y)∈U((a, b), δ) に対して、
|f(x, y)-f(a, b)| < ε」となるとき、f は S において連続であると定義します。
S = R2 のときに、この連続の定義を満たすと、f は R2 において連続ということになります。
先ほどの f(x, y) = xy が、この 2変数関数の連続性の定義を満たすことを後ほど証明します。
まずは、よく使う不等式の変形を使って、他の連続関数で、2変数関数の連続性を確認します。
2変数関数の連続性 :シンプルな例で連続性を示す練習
g : R2 → R を、
(x, y)∈R2 に対して、
g(x, y) = x2+y2 と定義します。
この z = g(x, y) という関数が、S = R2 において連続であることを定義に基づいて確認します。
任意に正の実数 ε と、
任意の (a, b)∈R2 が与えられたとします。
この ε と (a, b) に対して、
δ という正の実数を (ε/2)1/2 とします。
この δ = (ε/2)1/2 について、
U((a, b), δ) という点 (a, b) を中心とする δ-近傍を考えます。
δ = (ε/2)1/2 と設定したので、
U((a, b), δ) は、点 (a, b) を中心とする半径 (ε/2)1/2 の円の内部に含まれている点全体となっています。
任意の点 (x, y)∈U((a, b), δ) = U((a, b), (ε/2)1/2) に対して、
|g(x, y)-g(a, b)| の値と、ε との大小関係を考えます。
g の終集合である R における二点間距離は、絶対値を使って定義されています。
|g(x, y)-g(a, b)| は、一次元ユークリッド空間である R という数直線における二点間の距離となっています。
数直線において、g(x, y) という実数と f(a, b) という実数についての二点間の距離です。
任意の点という意味
「任意の点 (x, y)∈U((a, b), δ) = U((a, b), (ε/2)1/2) に対して、
|g(x, y)-g(a, b)| < (ε/2)1/2」ということを正しく理解することが大切になります。
「任意の点 (x, y)∈U((a, b), δ) = U((a, b), (ε/2)1/2) に対して、以下のことが成立する」ということは、「どんな点 (x, y)∈U((a, b), δ) = U((a, b), (ε/2)1/2) に対しても、以下のことが成立する」ということです。
ここで、U((a, b), δ) という集合に元(点)が含まれていることの定義を確認します。
δ = ε なので、
(x, y)∈U((a, b), δ) ということは、
(x, y)∈{(u, v)∈R2 | d((u, v), (a, b)) < δ} ということです。
今、(x, y)∈U((a, b), δ) なので、
d((x, y), (a, b)) < δ です。
d の定義から、
{(a-x)2+(b-y)2}1/2 < δ = (ε/2)1/2 です。
よって、
0 ≦ {(a-x)2+(b-y)2}1/2 < (ε/2)1/2 です。
各値を二乗しても、不等号の向きが変わらないことから、
(a-x)2+(b-y)2 < ε/2 … (1)
また、(a-x)2 = (a-x)2×1
= (a-x)2×(-1)2
= {(a-x)×(-1)}2 = (x-a)2
同様に、(b-y)2 = (y-b)2 です。
よって、これらを (1) に代入すると、
(x-a)2+(y-b)2 < ε/2 … (2)
さらに、(y-b)2 の値は 0 以上なので、この部分を足さないと値が低下する可能性が出てきます。
そのため、(2) より、
(x-2)2 ≦ (x-a)2+(y-b)2 < ε/2 です。
左辺と右辺を比べて、
(x-a)2 < ε/2 … (3)
また、(x-a)2 は 0 以上なので、(2) より、同様にして、
(y-b)2 < ε/2 … (4)
よく使う手
最終的に示したい不等式に使われる部分の式を見てみます。
|g(x, y)-g(a, b)| の値が気になるところです。
この値が 正の実数 ε 未満だということを示すと、連続であることの定義を満たしたことになります。
|g(x, y)-g(a, b)| を、2変数関数 g の定義に基づいて計算します。
|g(x, y)-g(a, b)|
= |(x2+y2)-(a2+b2)|
= |(x2-a2)+(y2-b2)|
≦ |x2-a2|+|y2-b2| … (5)
ここで、(3) と (4) から、
|x2-a2|+|y2-b2|
< ε/2+ε/2 = ε … (6)
(5) と (6) から、
|g(x, y)-g(a, b)| < ε
これで、z = g(x, y) という 2変数関数は、連続であることの定義を満たしました。
実は、先に |g(x, y)-g(a, b)| について様子を見ておいて、逆算しつつ、δ を設定しました。
先ほど使った、有名な不等式評価をまとめておきます。
(x, y)∈U((a, b), δ) という δ-近傍内の点について、
{(x-a)2+(y-b)2}1/2 < δ より、
(y-b)2 ≦ 0, (x-a)2 だから、
|x-a| < δ, |y-b| < δ となります。
ルートの中が文字の二乗のとき、絶対値をつけてルートを外すという高校の数学で学習した内容が効いています。
では、z = f(x, y) = xy が連続であることを示します。
2変数関数の連続性 :f(x,y)=xyは連続
【命題】
f(x, y) = xy という R2 を定義域とする 2変数関数の実数値関数は、R2 における任意の点において連続である。
<証明>
任意に正の実数 ε と任意の (a, b)∈R2 が与えられたとします。
δ = min{1, ε÷(1+|a|+|b|)} と置きます。
そして、任意に (x, y)∈U((a, b), δ) を取ります。
先ほど述べたことから、
|x-a| < δ, |y-b| < δ … (1)
ここで、次のような文字式の計算を頑張ります。
(x-a)(y-b)
= xy-xb-ay+ab … (2)
(x-a)b = xb-ab … (3)
a(y-b) = ay-ab … (4)
(2)+(3)+(4) の右辺は、
xy-xb-ay+ab+xb-ab+ay-ab
= xy-ab
(2)+(3)+(4) の左辺は、
(x-a)(y-b)+(x-a)b+a(y-b)
よって、左辺と右辺が等しいことから、
xy-ab =
(x-a)(y-b)+(x-a)b+a(y-b)
… ★
よって、★から、
|f(x, y)-f(a, b)|
= |xy-ab|
= |(x-a)(y-b)+(x-a)b+a(y-b)|
≦ |(x-a)(y-b)|+|(x-a)b|+|a(y-b)|
= |x-a||y-b|+|x-a||b|+|a||y-b|
ここで、(1) より、
|f(x, y)-f(a, b)|
< δ2+δ|b|+|a|δ
= δ×(δ+|a|+|b|)
ここで、δ = min{1, ε÷(1+|a|+|b|)} だったので、
δ ≦ 1 です。
括弧の中の δ を 1 で評価し、括弧の外の δ は δ のままにします。
すると、
|f(x, y)-f(a, b)|
< δ×(δ+|a|+|b|)
≦ δ × (1+|a|+|b|)
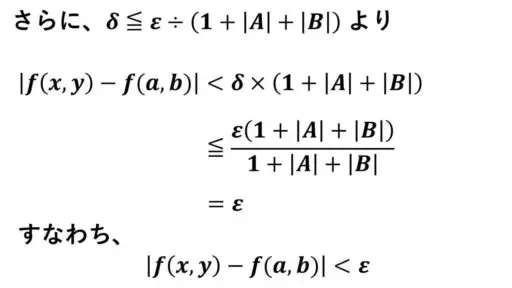
これで、
|f(x, y)-f(a, b)| < ε が示せました。
よって、
z = f(x, y) = xy は連続です。【証明完了】
今回の記事に関連する内容からの広がりについて述べておきます。
今回の記事の次の内容
f(x, y) = xy, g(x, y) = x2+y2 は、ともに R2 において連続でした。
ここで、(x, y) ≠ (0, 0) の範囲で、
z = f(x, y)÷g(x, y) という新しい 2変数の実数値関数を定義します。
z = xy÷(x2+y2) です。
ここで、(x, y) を (0, 0) に近づけるということを考えます。分子と分母が、どちらも 0 に近づくという不定形です。
実は、近づけ方によって、異なる収束値をもつことが分かります。
そのため、(x, y) → (0, 0) としたとき、
z = f(x, y)÷g(x, y) は極限値をもたないということになります。
近づけ方に依存せずに、同じ値に収束するときに限り極限値をもつと定義しています。
1 変数のときには、直線が定義域だったので、右から近づけるのと、左から近づけるという二つの接近の仕方でした。
右から近づけても、左から近づけても同じ値になるときに関数の極限値としたことを一般化したものになります。
定義域が R2 である 2変数の実数値関数のときは、片方の点をもう片方の点に近づける近づけ方が無数にあります。
そのため、δ-近傍を使った連続性の定義では、近づけ方を指定していません。
近づけ方に依存することなく、
任意の (x, y)∈U((a, b), δ) に対して、
|f(x, y)-f(a, b)| < ε を示すことが、2変数関数の連続性の証明となります。
z = xy÷(x2+y2) の (x, y) = (0, 0) における値を 0 だと定義すると、R2 における任意の点で偏微分可能ということが証明できます。
しかし、(0, 0) という点において、連続ではないということを関連記事で示しています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。