黄金比 | 正五角形の一辺の長さと対角線の比【円に内接している状況から角度を計算】
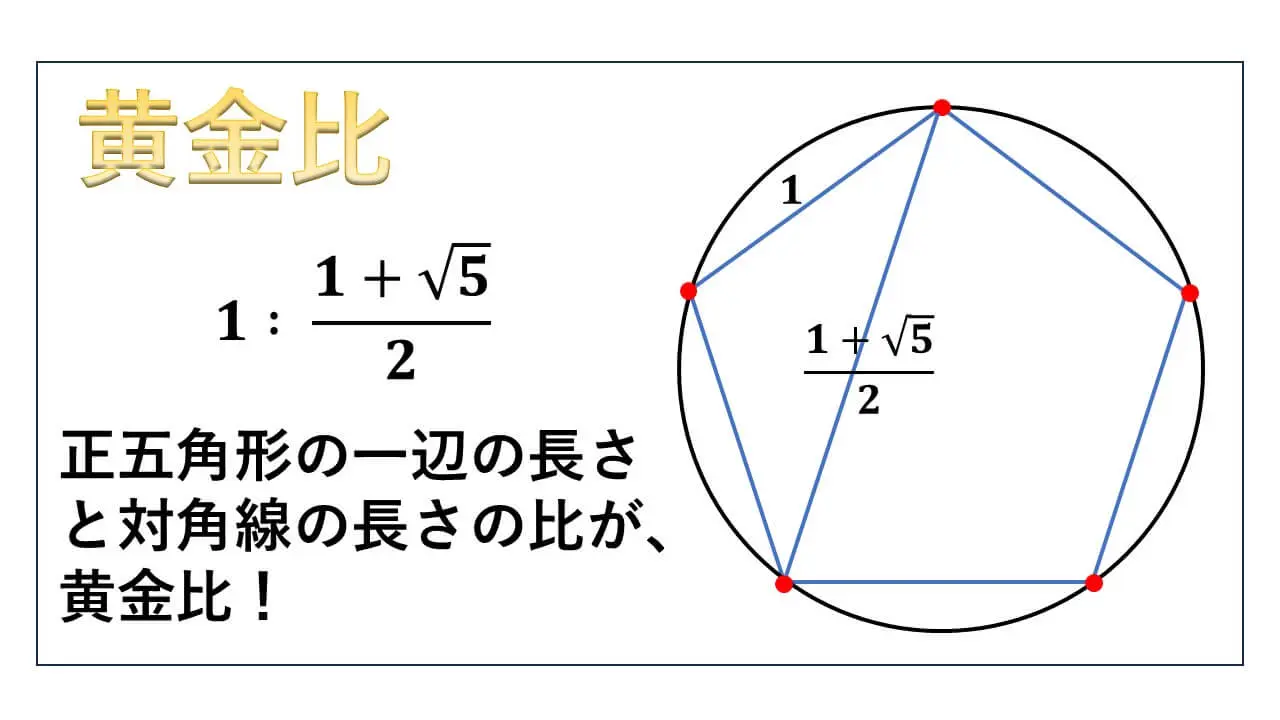
正五角形の一辺の長さと対角線の長さの比が" 黄金比 “となっていることを解説します。
決め手になるのが、相似な三角形の対応する辺の長さの比が等しいということです。
ただ、三角形が相似ということを示すために、角度の大きさを正確に計算するという土台作りが大切になります。
黄金比は、パリの凱旋門やパルテノン神殿、モナリザといった有名な美術・建造物に利用されています。
高校の世界史だと、アテナイやパルテノン神殿の場所を押さえているかどうかを試す地図を使った問題が出題されることもあるかと思います。
この記事では、数学の記事ですので、中学もしくは高校の数学で、図形の角度を弧の長さから正確な理論から計算し、その値を根拠に三角形の相似へと議論を進めます。
まずは土台となる角度の大きさの把握です。弧の長さから扇形の中心角の大きさをクッションにして、円周角の大きさを計算します。
黄金比 :等しい弧の長さから
一辺の長さが 1 の正五角形ABCDE が円O に内接している状況を考えます。
ここで、"正"五角形なので、各頂点が円周の長さを、ちょうど五等分しています。
Just 五等分ということから、例えば、扇形OCD と扇形ODE が合同です。
これは、扇形の半径が同じ円の半径で、弧の長さが同じ長さだからです。
このように考えると、イタリアで有名な食べ物のピザを、中心O のまわりに 5 等分できます。
360° を 5 等分したうちの一つは 76° です。
ここで、同じ弧に対する中心角の大きさの半分が、その弧に対する円周角の大きさです。
そのため、弧CD に着目すると、
中心角である ∠COD の半分が、
円周角 ∠CAD の大きさです。
弧BC や弧DE について同様に考えると、中心角である 72° の半分の大きさが、円周角の大きさです。
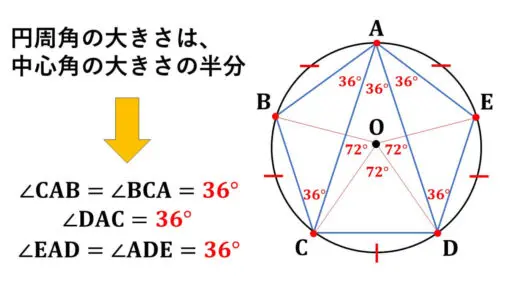
まとめると、
∠CAB = 36°,
∠DAC = 36°,
∠EAD = 36° となっています。
よって、∠BAE という五角形の一つの内角が、対角線 AC と 対角線 AD によって、三等分されていることが分かります。
弧AB や弧EA の長さも、弧BC たちと同じく円周を五等分してできた長さなので、円周角の大きさは同じ大きさとなっています。
そのため、
∠BCA = ∠ADE = 36° です。
ちなみに、正五角形の 5 つの内角の大きさはどれも同じなので、正五角形の一つの内角の大きさを次のように計算で求めることができます。
今、正五角形は、△ABC, △ACD, △ADE の三つに分けられています。
そのため、正五角形の 5 つの内角の和は、三つの三角形の内角の和と等しい状態になっています。
一つの三角形の内角の和は 180° なので、正五角形の 5 つの内角の和は、その 3 倍となっています。
つまり、
180° × 3 = 540° が、正五角形の 5 つの内角の和です。
5 つの内角は、どれも同じ大きさなので、正五角形の一つの内角の大きさは、540° を五等分したうちの一つということになります。
540° ÷ 5 = 108° より、
正五角形の一つの内角の大きさが 180° と分かりました。
ここまでの議論を高校の数学IIの公式を使うと、もっと速く計算することができます。
数学II を履修したことがある方用に、その計算方法を述べておきます。
数学II を履修していない方は、次の部分を飛ばして、ご覧ください。
数学IIの公式を使って速く計算
【弧の長さの公式】
半径 r, 中心角 θ ラジアンの扇形の弧の長さを l とする。
このとき、l = rθ
ブログ弧度法より
先ほどの円に内接している五角形について、5 つの扇形の半径は、どれも同じ円 O の半径で一定です。
そして、円周を五等分したうちの一つが扇形の弧の長さなので、l の値も一定です。
そのため、扇形の中心角 θ の値は、どれも同じ値となっています。
つまり、θ = l ÷ r より、5 つの扇形の中心角は、どれも等しくなっています。
よって、円周角は中心角の大きさの半分なので、等しい弧についての円周角の大きさが、どれも等しいということが分かります。
そのため、∠BAE という五角形の一つの内角が、対角線 AC と 対角線 AD によって、三等分されていると、すぐに判断できます。
計算すると、
∠CAB = ∠DAC = ∠EAD
= 108° ÷ 3 = 36° です。
※ ラジアンと度数の対応から、度数にしても三等分されています。
もちろん数学II を使わなくても、中学一年で学習する扇形の弧の長さの公式から、同様の内容が導けます。
それでは、さらに角度の計算を進めて、相似な三角形を見つけます。
黄金比 :角度から相似へ
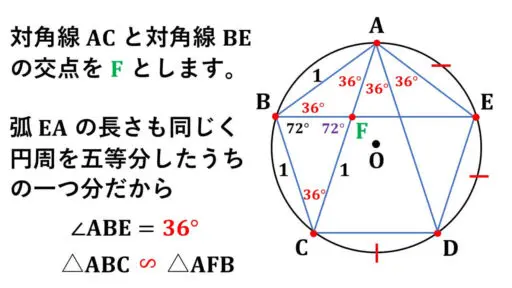
さらに、対角線 BE を引きます。
弧AE の長さも弧CD と同じ長さだったので、弧AE に対する円周角の大きさも同じ大きさです。
つまり、∠ABE = 36° です。
すると、二組の角の大きさが等しいので、相似条件を満たし、二つの三角形が相似ということが分かります。
△ABC ∽ △AFB となっています。
∠BAC = ∠FAB = 36°,
∠BCA = ∠FBA = 36° が二組の角がそれぞれ等しいということです。
さらに、正五角形の一つの内角は 108° なので、
∠CBF = ∠ABC - ∠ABE
= 108° - 36° = 72° です。
そして、三角形の内角の和が 180° ということから、
∠CFB = 180°- (72°+36°)
= 72° です。
そのため、∠CBF = ∠CFB より、
△CFB は二等辺三角形となっています。
はじめの設定で、正五角形の一辺の長さは 1 でした。
そのため、CF = CB = 1 です。
正五角形の対角線の長さは、まだ未知数なので、x と置いておきます。
正五角形の一辺の長さは 1 で、対角線の長さが x です。
そのため、正五角形の一辺の長さと、対角線の長さの比は、
1 : x ということになります。
この x の値を求めたいので、x を用いた方程式を作ることを目指します。
対角線AC の長さが x なので、
AF = AC - CF
= x - 1 となります。
ここで、相似な三角形の対応する辺の長さの比が等しいということを使います。
相似比から二次方程式へ
△ABC ∽ △AFB より
AB :AF = AC : AB です。
AB = 1, AC = x, AF = x-1 を代入すると、次のようになります。
すなわち、
1 : (x-1) = x : 1 です。
内項の積と外項の積が等しいため、
x(x-1) = 1 です。
これで、x についての二次方程式が得られました。
展開して整理すると、
x2-x-1 = 0 となります。
正五角形の一辺の長さと、対角線の長さの比が
1 : x ということで、x の値を求めたかったのですが、これで二次方程式を解の公式で計算し、x の値を求めることができます。
x は対角線の長さなので、0 よりも大きいということに注意して、次のように値を求めます。
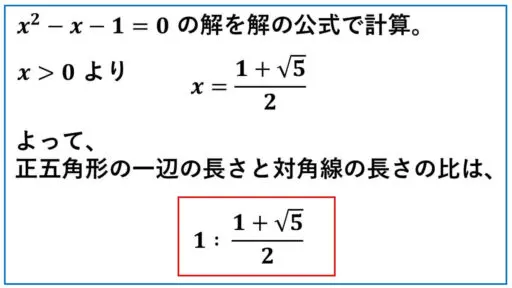
この比が黄金比です。
正五角形の一辺の長さと対角線の長さの比が、黄金比となる具体例の一つです。
今回の記事では、図形を使って、弧の長さから中心角や円周角の大きさを計算することで、相似な三角形を見つけ黄金比となっていることを示しました。
未知数である対角線の長さを x と置き、x を用いた方程式を解くことで x の値を決定するという中学や高校の数学で学習する議論の流れでした。
黄金比ですが、高校の数学では数列単元で、発展的な内容ですが漸化式と関わってきます。
フィボナッチ数列という記事で、その内容を解説しています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。
