ねじれ群 | ねじれ部分群で剰余群をつくると、ねじれのない群になることの証明

" ねじれ群 – ねじれ部分群 “について、基本となる内容を解説しています。
ねじれ部分群でコセットを考えるということから議論を広げます。
ねじれ元とは、元の位数が有限の元のことです。
有限位数の元全体が部分群になること、そしてコセットを考えるとどうなるのかを説明します。
それでは、ねじれ元の定義から説明します。
ねじれ群 :ねじれ元の定義から
群 A を加法群とします。
A の元 x の位数が有限であるときに、x を A のねじれ元といいます。
位数が有限ということは、ある正の自然数 n が存在し、
nx = 0 となります。
0 ∈ A は、n = 1 の段階で既に 0 なので位数 1 と有限です。
そのため、必ず加法群には、少なくとも一つはねじれ元が存在します。
そこで、加法群 A のすべてのねじれ元を全部集めた部分集合 T を定義することができます。
この T は A の部分群です。
実際、x, y ∈ T とすると、T の定義から x と y の位数が有限なので、ある正の整数 m と n が存在し、
mx = 0, ny = 0 となります。
よって、
(mn)(x-y)
= n(mx)-m(ny) = 0-0 = 0
x – y の位数が有限なので、
x – y ∈ T となり、T は部分群です。
この部分群 T を A のねじれ部分群といいます。
T が全体 A に一致しているときは、A をねじれ群といいます。
このときは、加法群 A のすべての元が有限位数ということです。
なお、0 ∈ T なので、どんな加法群についても、必ず T は空集合ではありません。
また、アーベル群の二項演算は可換なので、どんな部分群も正規部分群です。
そのため、コセットを考え、剰余群を定義することができます。
コセットを考えると
T をアーベル群 A のねじれ部分群とします。
T は A の正規部分群なので、コセットを考えて剰余群を定義できます。
A/T という剰余群についての基本となる定理を証明します。
言葉の注意ですが、加法群 A の元について、有限位数の元が零元 0 のみのとき、A はねじれがない群といいます。
【定理1】
T を加法群(アーベル群)A のねじれ部分群とする。
このとき、
剰余群 A/T は、ねじれのない加法群である。
<証明>
もし a + T ∈ A/T (a ∈ A かつ a は T の元ではない)の位数が有限だったとします。
a が T の元ではないので、T の定義より、a の位数は有限位数ではありません。
一方、A/Tにおいて、
a+T の位数が有限より、
ある正の整数 n が存在し、
n(a + T) = 0 + T
これは、(na) + T = 0 + T ということなので、
na = na + 0
∈ {na + x | x ∈ T} = (na) + T
また、n(a + T) = (na) + T であり、
(na) + T = 0 + T なので、
na ∈ (na) + T
= 0 + T = { 0 + x | x ∈ T}
よって、ある y ∈ T が存在して、
na = 0 + y = y ∈ T
na ∈ T より、T の定義から、
na は有限位数なので、ある正の整数 k が存在し、
k(na) = 0
これは、(kn)a = k(na) = 0 ということなので、a が位数有限であることを示しています。
しかし、a の位数は有限位数ではなかったので、矛盾です。
よって、A/T の零元 0 + T を除く全ての元について、位数が有限ではないということが示せました。
つまり、A/T はねじれのない群です。【証明完了】
この【定理1】から、ねじれ部分群 T について A/T を考えると、ねじれ元を分断できることが分かりました。
さらに、ねじれのない加法群について成立する定理を示します。
ねじれがないとき
【定理2】
ねじれがない有限生成アーベル群 A は、有限階数の自由アーベル群である。
この証明は、補足ノート4という記事で述べています。
【定理1】と【定理2】を合わせると、次の定理が得られます。
ねじれ群 :コセットを利用して分解
【定理3】
A を有限生成アーベル群とし、T を A のねじれ部分群とする。
このとき、A は T と A/T の外部直和に同型である。
<証明>
記号ですが、A/T の元 x + T のことを x’ と表すことにします。
【定理1】より、A/T はねじれがない有限生成アーベル群です。
そのため、【定理2】より、有限階数の自由アーベル群となっています。
{a1', … , an'} を A/T の基底とします。
そして、f : A → A/T を自然な全射準同型写像とします。
すなわち、a ∈ A に対して、
f(a) = a’ = a + T です。
ここで、f が全射であることから、A/T の基底を構成する各元 ai' について、
f(ai) = ai' となる ai ∈ A となっています。
※ ai' ≠ 0’ なので、ai の元の位数は有限ではありません。
今、A/T の代表元を a1, … , an に固定します。
すると、{a1', … , an'} が基底なので、
g : A/T → A を
g(z1a1'+…+znan')
= z1a1+…+znan(各 zi は整数)と定義することができます。
※ 基底の取り方に依存する写像 g です。
合成写像 fg は A/T から A/T への恒等写像となっています。
このことから、g は単射ということになります。
実際、x’, y’ ∈ A/T に対して、
g(x’) = g(y’) とし、これらを f で移すと、
(fg)(x’) = (fg)(y’)
fg が恒等的なので、x’ = y’ となり、g が単射ということになります。
そのため、Im g = g(A/T) は A/T と群として同型になっています。
※ Im g を B と置きます。
{a1, … , an} は B を生成していますが、全体 A を生成しているかは定かではありません。
しかし、A が有限生成という仮定から、有限個の元を補充すると、A の生成系とすることができます。
{a1, … , an, b1, … , bi} を A の生成元とします。
すると、A の任意の元 x はこれらの一次結合で表され、b1 + T, … , bi + T が 、
{a1', … , an'} という A/T の基底の一次結合で表されるので、次のようになります。
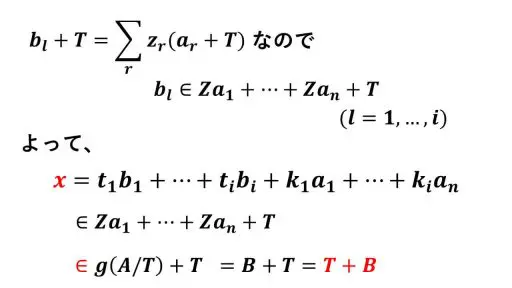
これは、A = T + B ということを示しています。
さらに、x ∈ T ∩ B とすると、x ∈ B だから、
ある a + T ∈ A/T が存在して、
x = g(a + T) … (1)
x ∈ T だから、f(x) = 0 + T なので、
0 + T = f(x)
= fg(a + T) = a + T
よって、
g(a + T) = g(0 + T) = 0
(1) より、x = g(a + T) = 0
したがって、T ∩ B = {0}
これは、A = T + B が内部直和ということを示しています。
よって、B が A/T と群として同型だったので、
A は T と A/T の外部直和と群として同型になります。【証明終了】
さらに、T が有限群だということが分かります。
T の位数が有限な理由
有限生成アーベル群 A のねじれ部分群 T は、位数が有限な有限群ということまで決定できます。
今、証明した定理から、A は T と A/T の外直和(外直積)と群として同型です。
A から T と A/T の外直積への群同型写像を Ψ とします。
そして、 T × A/T の元 (t, a + T) に対して、
t ∈ T を対応させるという射影を p とします。
Ψ と p で写像を合成すると、
A から T × A/T を経由して T への群準同型写像となります。
よって、p(Ψ(A)) = T となります。
A が有限生成なアーベル群だったので、
p(Ψ(A)) = T も有限生成です。
そして、T のどの元の位数も有限というねじれ部分群の定義から、
位数 | T | が有限と結論づけられます。
有限個の生成元の元の位数が有限なので、生成されている集合 T は、有限個の元となっているということです。
このねじれ群 T は有限生成アーベル群のねじれ群です。
そのため、A が有限生成ということと全射準同型像の関係から、T が有限群ということを導けました。
つまり、有限生成のアーベル群が有限階数の自由アーベル群とねじれ群の直和に分解することが分かりました。
ここからは、有限生成アーベル群のねじれ部分群がアーベルp群の直和に分解することを説明します。
記号の導入から始めて
上で示した【定理3】によって、有限生成アーベル群は、ねじれ群 T と剰余群 A/T に直和に分けられています。
そして、A/T は有限階数の自由アーベル群です。
そのため、有限位数のねじれ群 T の構造を調べます。
【記号の導入】
有限位数のアーベル群 A と素数 p について、元の位数が p のべきとなっている A の元をすべて集めた集合を T(p) と表すことにします。
※ ただし、どの素数 p についても T(p) に 0 を含めておくこととします。
この T(p) は、A の部分群となっています。
そのことを次で証明します。
実際に確認
【命題】
アーベル群 A の元で、元の位数が素数 p のべきとなっているものが少なくとも 1 つは存在したとする。
このとき、T(p) は A の部分群である。
<証明>
x, y ∈ T(p) とし、x と y の元の位数をそれぞれ a と b とします。
ここで、max{a, b} = c と置きます。
すると、
pc(x – y) = pcx – pcy = 0 – 0 = 0 となり、x – y の位数も素数 p のべきということになります。
よって、x – y ∈ T(p) となり、T(p) が A の部分群であることが証明できました。【証明完了】
この T(p) は、どの元の位数も素数 p のべきで、p ではない他の素数が使われていません。
シローの定理に関連する考察をすると、
T(p) の位数が p とは異なる素数 q を素因子としてもつと、元の位数が q となっている元が T(p) の中に含まれることになります。
しかし、T(p) のどの元も、元の位数が p べきなので、そのようにはなっていません。
そのため、T(p) は p 群ということになります。
では、有限位数のアーベル群の構造へと切り込みます。
位数有限のアーベル群は、アーベルp群の直和に分解します。
ダイレクトサムになる
【定理4】
A を有限位数のアーベル群とし、A の各元に現れる素因子のすべてが、p1, … , pn だとする。
このとき、
A = T(p1)+…+T(pn) であり、しかも、これは直和である。
<証明>
まずは、T(p1) + … + T(pn) が A と等しいことを示します。
A の各元の位数に現れる素因子全体を P と置きます。
P = {p1, … , pn} という有限集合になっています。
p ∈ P とすると、P の定め方から、p は A のある元 a の位数の素因子となっています。
a の元の位数を r とすると、r = pk (k は整数) と表せ、
ka ≠ 0, p(ka) = 0
つまり、0 ≠ ka ∈ T(p) となります。
T(p) ≠ {0} だと位数 p の A の元は存在するので、
p ∈ P と T(p) ≠ {0} が同値となります。
任意の a ∈ A について、a の元の位数を r とします。
そして、r の素因数分解を
r = pk1pk2 … pks とします。
(ただし、s ≦ n です。)
qi = r ÷ pki (i = 1, 2, … , s) と置きます。
gcd(q1, … , qs) = 1 となっているので、
ある整数 m1, … , ms が存在して、
1 = m1q1 + … + msqs
※ 最大公約数という記事の最後で、この内容を示しています。
よって、
a = 1a = (m1q1 + … + msqs)a
= m1q1a + … + msqsa
ここで、
pi(miqia) = {mi(piqi)}a = mira = 0 なので、
miqia ∈ T(pi) です。
これで、A の任意の元 a が、
T(p1) + … + T(ps) という部分群に含まれることが示せました。
s ≦ n なので、
A = T(p1) + … + T(pn)
次に、これが内直積(内直和)となっていることを示します。
その証明
ai ∈ T(pi) について、
a1 + … + an = 0 だとします。
a1 = … = an = 0 ということを示せば、A の元の表し方が一意的ということになり、直和であることが示せたことになります。
各 ak の元の位数を pktk という p べきだとし、
1 ≦ i ≦ n である任意の i について、
p1t1×…×pk-1tk-1×pk+1tk+1×…×pntn を qi と置きます。
piti と qi の最大公約数は 1 なので、
ある整数 x と y が存在して、
xpiti + yqi = 1 となります。
つまり、
ai = (xpiti + yqi)ai
= xpitiai + yqiai
ここで、
ai = -a1– … -ai-1 – ai+1 – … – an
そして、各 ak の元の位数が pktk から、
pktkak = 0 なので、
ai = xpitiai + yqiai = 0 + yqiai
= yqi(-a1– … -ai-1 – ai+1 – … – an)
p1t1×…×pk-1tk-1×pk+1tk+1×…×pntn が qi だったので、
k ≠ i のとき、
qiak = 0 ということから、ai = 0
1 ≦ i ≦ n の任意の i について、ai = 0 が示せたので、
T(p1) + … + T(pn) が直和であることが示せました。【証明終了】
アーベルp群群の直積に分解するということが示されました。
【補足】
★については、
x1 + … + xn = y1 + … + yn
とすると、右辺を左辺に移項して、
(x1 – y1) + … + (xn – yn) = 0
ai として xi – yi と見ると、★より、
ai = 0 となるので、xi = yi となり、表し方の一意性が従います。
この内容まで押さえると、有限生成アーベル群の構造がかなり見えてきます。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。