3倍角の公式 | tan、sin、cosについての証明【4倍角の公式も】

" 3倍角の公式 “を、sin、cos、tan について証明しています。また、同じ要領で4倍角の公式も証明しています。
特にsinとcosについての3倍角の公式は、数学IIBだけでなく、数学IIICでも使うので、押さえておくと良いかと思います。
自分で公式を導けるようになっておくと、忘れても復元できますし、公式を導くこと自体が、三角関数についての計算の良い練習になります。
sin 3x, cos 3x の公式を証明してから、tan 3x の公式を証明します。
3倍角の公式 :まずはsinとcosから
【加法定理】
ブログ複素三角関数の加法定理より
sin(θ1+θ2)=sinθ1cosθ2+cosθ1sinθ2
cos(θ1+θ2)=cosθ1cosθ2-sinθ1sinθ2
まず、sin についての3倍角の公式を証明します。
その後に、sinのときの結果を使って、cosの3倍角の公式を導きます。
数学では、既に成立している命題を利用して、議論をさらに進めることをよくします。
【sinの3倍角の公式】
x を実数とすると、
sin 3x = 3sin x -4sin3x
<証明>
sin 3x = sin(x + 2x) なので、この右辺に加法定理を使います。
sin 3x = sin(x + 2x) =
sin x cos 2x + cos x sin 2x =
sin x (cos x cos x - sin x sin x)
+ cos x(sin x cos x + cos x sin x) =
sin x(cos2x -sin2x) + 2sin xcos2x
ここで、
cos2x = 1 - sin2x なので、
cos2x -sin2x = 1 - 2sin2x だから、
sin 3x =
sin x - 2sin3x + 2sin x(1 - sin2x)
よって、sin 3x = 3sin x - 4sin3x【証明完了】
加法定理を使って、sin 3x の公式を導きましたが、数Cのド・モアブルの定理を使っても導くことができます。
この sin 3x の3倍角の公式から、cos 3x が導かれます。
cos についての加法定理から導くこともできますが、sin のときと同じような内容なので、違ったアプローチをしてみます。
cos3xはsin3xから
【cosの3倍角の公式】
x を任意の実数とすると、
cos 3x = -3cos x + 4cos3x
<証明>
x を任意の実数とします。
θ = x + π/2 について、
sin 3θ = 3sin θ - 4sin3θ
= sin(x + π/2)-4{sin(x + π/2)}3 … ★
ここで、
sin (x + π/2) = sin x cos π/2 + cos x sin π/2
つまり、
sin (x + π/2) = cos x … (1)
さらに 3 乗すると、
{sin(x + π/2)}3 = cos3x … (2)
(1) と (2) を ★に代入すると、
sin 3θ = 3cos x - 4cos3x … ■
一方、
sin 3θ = sin{3x + (3/2)π}
= sin 3x cos{(3/2)π}+cos 3xsin{(3/2)π}
= sin 3x × 0 + cos 3x × (-1)
= -cos 3x
これを ■ へ代入すると、
-cos 3x = 3cos x - 4cos3x
つまり、
cos 3x = -3cos x + 4cos3x【証明完了】
ここからは、tan の3倍角の公式を証明します。
tan3xの3倍角の公式

これで、tan 3x についての3倍角の公式の証明が完了しました。tan についての加法定理から導いています。
図の右上の赤色で囲った等式が、tan(x + x) に加法定理を適用した結果です。
tan(x + 2x) に加法定理を使い、途中式に現れる tan2x に角が x の式に書き換えます。
(1 - tan2x)/(1 - tan2x) は 1 なので、掛けても値が変わらないことから、真ん中の二つの式の書き換えています。
では、次に4倍角の公式について証明します。
3倍角の公式の証明と同じように、加法定理を使って証明できます。
3倍角の公式 :4倍角の公式も
【sinの4倍角の公式】
x を任意の実数とすると、
sin 4x = cos x(4 sin x - 8sin3x)
<証明>
ここで、倍角の公式ですが、
sin 2x = 2sin x cos x,
cos 2x = 1 - 2sin2x です。
※ 倍角の公式も加法定理を計算した結果です。
これらを用いると、
sin 4x = sin(2x + 2x)
= sin 2x cos 2x + cos 2x sin 2x
= 2sin 2x cos 2x
= 4sin x cos x(1 - 2sin2x)
= cos x(4sin x - 8sin3x)【証明完了】
cosの倍角の公式ですが、
1 - 2sin2θ = 1 - 2(1 - cos2θ) なので、
cos 2θ = 2cos2θ - 1 にもなります。
この形のcosの倍角の公式を θ が 2x のときに使うと、cosについての4倍角の公式が導けます。
【cosの4倍角の公式】
x を任意の実数とすると、
cos 4x = 8cos4x - 8cos2x + 1
<証明>
cos についての倍角の公式から、
cos 4x = cos(2x + 2x)
= 2cos22x - 1
ここで、再び、倍角の公式から
cos 2x = 2cos2x - 1 なので、
この両辺を二乗してから 2 倍すると、
2cos22x = 2(2cos2x - 1)2 です。
よって、
cos 4x
= 2(2cos2x - 1)2-1
= 8cos4x-8cos2x + 1【証明完了】
では、tanについても4倍角の公式を証明します。
tanの4倍角の公式
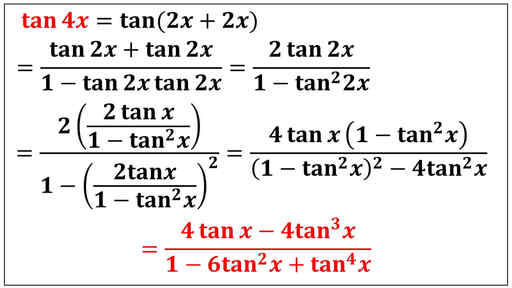
これが証明になります。
tan(2x + 2x) に加法定理を使い、
tan 2x を先ほどの tan の3倍角の公式を導いたときと同じように書き換えます。
(1-tan2x)/(1-tan2x) の値が 1 なので、掛けても値が変わらないことから、下から二行目の式を書き換えています。
tan については、3倍角と4倍角の公式を加法定理の練習に述べましたが、sinやcosは数学IIIでよく使います。参考程度に、積分で使う例を述べておきます。
3倍角の公式 :積分で使用(数III)
【練習問題】
次の不定積分を ∫cos3x dx を求めてください。
∫ cos kx dx = 1/k × sin kx + C (C は積分定数)と計算できます。しかし、3 乗などの指数については、うまくいく公式がありません。
そこで、3倍角の公式を使って、3 乗が出ない 1 乗の形に式を書き換えます。
cos 3x = 4cos3x - 3cosx だったので、
cos3x = 1/4(cos 3x + 3cos x) として不定積分を計算します。
C を積分定数として、
∫cos3x dx =
1/4∫(cos 3x + 3cos x)dx =
(1/12)sin 3x+(3/4)sin x+C
sin3x の積分についても、同じように、3 乗が出ない 1 乗の形に式を書き換えて計算をします。
sinについても積分
【練習問題】
次の不定積分を ∫sin3x dx を求めてください。
C を積分定数とします。
sin 3x = 3sin x - 4sin3x だったので、
sin3x = 1/4(3sin 3x - sin 3x) だから、
∫sin3x dx =
1/4∫(3sin 3x - sin 3x)dx =
-(3/4)cos 3x + (1/12)cos 3x + C
数学IIIで、3倍角の公式を使うと、うまく計算ができるときもあるので、押さえておくと良いかと思います。
高校数学についての記事を他にも投稿しています。
和積変換公式という記事で、sinやcosについての数IIの内容を解説しています。
数学IIの公式は、よく使うので具体的な値を用いて練習し、いつでもスムーズに公式を使えるようにしておくことが大切になります。
読んで頂き、ありがとうございました。
これで、今回のブログ記事を終了します。