平行線と線分の比 – メネラウスの定理 – 高校 | 比の値を用いて平面図形の証明
" 平行線と線分の比 " に関連して、高校の数学の証明では、比の値についての情報を図形から引き出しつつ、さらに計算規則と合わせて結論を導くことをしばしば行います。
線分の長さが正の実数であるということから、比の値という正の実数についての計算が使えます。
高校の平面図形の単元で学習するメネラウスの定理を、平行線と線分の比の観点から証明しています。
この記事では、２点 A, B を結んだ線分の長さを AB というように表しています。
AB と BA は同じ線分の長さなので、等しい正の実数となっています。
適宜、AB と BA を書き換えることを行うので、その際は同じ長さということによる書き換えになります。
平行線と線分の比 :準備の内容
算数で比を学習したときに、身近な事柄を通して、「ミリンと醬油を 2 : 3 で混ぜる」というようなことを学習します。
この a : b = c : d という表し方は、相似な三角形について、どの線分と線分の長さが対応しているのかということを把握するのに役立ちます。
さらに、比の値を考えることができます。
高校の平面図形で登場する線分の長さは、正の実数値となっています。
正の実数なので、分数の分母に置くことができます。
AB : CD = EF : GH だと、
AB/CD = EF/GH と比の値の形で表すことができます。
この分数の形にしておくと、実数なので、実数についての計算規則に基づいて議論を進めることができます。
図形からの情報にプラスアルファして、実数についての計算で議論を進めるのが常套手段となります。
この例として、メネラウスの定理を証明します。
図形の用語に慣れておく
直線（線分）についての議論を今回の記事で扱います。
ここで、同一の平面上にある異なる２点が与えられているときに、その２点を通る直線が１本だけ存在するということになります。
直線（線分）が出てきたら、どういう点を通っているのかということを意識すると良いかと思います。
異なる２点 A, B に対して、直線AB は、端点 A と B を、どちらも貫通して理論上は永遠に線が伸びている状態です。
それに対して、線分AB は、端点 A と B を結んだ線で、どちらの端点も貫通していない状態になります。
三角形ABC が与えられているときには、三角形の３辺は、どれも線分ということになります。
ただし、線分AB などの辺について、端点を貫通した（半）直線を考えるときもあります。
その際には、辺AB の延長という言い方をします。
それでは、平行線と線分の比についての準備となる内容を述べたので、ここからはメネラウスの定理の証明を解説します。
メネラウスの定理は、与えられた１個の三角形と、その３つの頂点を通らない１本の直線についての定理になります。
高校の数学なので、この状況について場合分けが発生します。
平行線と線分の比 :メネラウスの証明
三角形ABC と、その三つの頂点 A, B, C のどの点も通らない直線 l が与えられたというのがメネラウスの定理の仮定になります。
この仮定を満たす状況を場合分けして考えます。
【３辺との交点が 0 個】という場合が考えられます。
この場合については、３辺をすべて延長して、直線 l との交点を考えることになります。
辺の外分点が３個という状況になります。
三つの頂点を通らないという仮定条件から、辺AB と辺 CA について l との交点が A のみという場合は除外されます。
同じく l との交点が B のみ、C のみという状況も除きます。
さらに、三角形と直線の交点ですので、l と３辺がそれぞれ１点ずつ交点をもつということは起こりません。
よって、残された可能性は、【３辺との交点が 2 個】という場合になります。
どちらの場合についても、若干の表面的な言葉の調整だけなので、本質的には同じ証明の内容となります。
ここからは、今の考察で得た２つの場合についての図を用いて、メネの証明について述べます。
定理の証明
【定理】
三角形ABC と、点 A, B, C のいずれも通らない直線 l が与えられたとする。
そして、辺BC, CA, AB もしくは、その延長と l との交点をそれぞれ P, Q, R とする。
このとき、
BP/PC・CQ/QA・AR/RB = 1 となる。
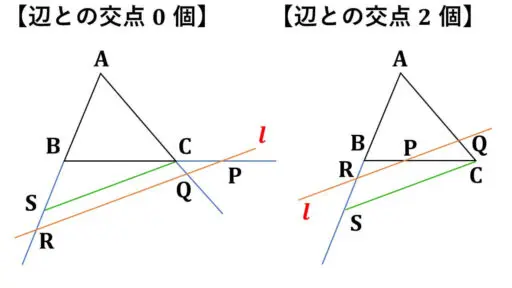
※ 点 C を通り直線 l に平行に引いた緑の補助線と直線AB との交点を S としています。
＜証明＞
まず【辺との交点 0 個】の場合を示します。
CS と l が平行なので、同位角が等しいことから、次の三角形が相似になります。
三角形BRP と三角形BSC が相似となっています。
ここで、
中学で学習した内容から、
BP : PC = BR : RS です。
そのため、比の値について、
BP/PC = BR/RS …①
次に三角形ARQ と三角形ASC に注目します。
やはり、
中学で学習した内容から、
CQ : QA = SR : RA となっています。
比の値について、
CQ/QA = SR/RA …②
①と②という実数についての等式を辺々掛け合わせます。
すると、
BP/PC・CQ/QA
= BR/RS・SR/RA です。
AR/RB は実数なので、こうして得たこの等式の両辺に掛けることができます。
よって、
BP/PC・CQ/QA・AR/RB
= BR/RS・SR/RA・AR/RB
= BR/SR・SR/AR・AR/BR
= BR/AR・AR/BR
= BR/BR = 1 です。
同じ線分の長さが分母と分子に置かれいるので約分されて、示したい結論の等式が得られました。
残りの場合についても同じ要領で証明をすることができます。
残りの場合も証明
次に【辺との交点 2 個】の場合を示します。
三角形BRP と三角形BSC の部分について、先ほどと同様に中学で学習した内容を使います。
BP/PC = BR/RS …③
また、三角形ARQ と三角形ASC の部分に中学で学習した内容を使います。
CQ/QA = SR/RA …④
③と④を辺々掛け、
BP/PC・CQ/QA
= BR/RS・SR/RA を得ます。
AR/RB を両辺に掛け、
BP/PC・CQ/QA・AR/RB
= BR/RS・SR/RA・AR/RB
= BR/SR・SR/AR・AR/BR
= BR/AR・AR/BR
= BR/BR = 1 【証明完了】
これで、メネの定理を証明することができました。
今の証明では、頂点 B から左回りに一回りするように考えました。
三角形が出てきたら、どの頂点からでも良いので、１つの頂点を決めてから、落ち着いて議論を１周させると良いかと思います。
定理の逆も証明
【メネラウスの定理の逆】
三角形ABC の辺BC, CA, AB もしくはその延長線上に３点 P, Q, R があるとする。
そして、
BP/PC・CQ/QA・AR/RB = 1 となっていたとする。
このとき、P, Q, R は同一直線上にある。
＜証明＞
BC と QR の交点を P’ と置きます。
この P’ が与えられた点 P と一致していることを示します。
仮定より、
CQ/QA・AR/RB
= PC/BP …①
また、メネラウスの定理より、
BP’/P’C・CQ/QA・AR/RB
= 1 …②
①を②に代入すると、
BP’/P’C・PC/BP = 1 です。
つまり、
BP’/P’C = BP/PC です。
点 P’ と点 P は BC 上の点なので、分点比が等しいことから一致しています。
P’ は直線QR 上の点でした。
P と P が一致しているので、点 P は直線QR 上にあるということになります。
これで、P, Q, R が同一直線QR 上にあることが示せました。【証明完了】
今回、平面図形の有名な定理を証明しました。
三角形ABC と、直線 l との分点を P, Q, R と規則的にアルファベット順に設定をしていました。
しかし、実際は、使われるアルファベットが不規則なものとなっているので注意です。
【関連する記事】
■ 三角形の面積比（チェバの証明）
■ 方べきの定理
今回の証明でも使った「比が等しい」ということの定義については、比の相等という記事で解説をしています。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。