デデキント切断 | 定義と具体例を述べた後で比較的に同値であることを示せる公理を一つ
" デデキント切断 “に関連した実数の連続性の公理に関わる内容を解説しています。
デデキント切断の定義を述べた後、具体例を示しつつ、ワイエルシュトラスの上限公理を認めてからデデキントの切断公理を導きます。
その後で、デデキントの切断公理を認めてからワイエルシュトラスの上限公理を導きます。
この二つが同値であることは、他の公理と同値であることを示すことを考えると比較的に楽かと思います。
実数の連続性の公理に関連して、微分積分学の基礎的な土台となる理論を学習する際に、上界と上限に慣れるのに良い内容かと思います。
この記事では、実数全体から成る集合を R と表すことにします。
デデキント切断 :定義と具体例
【定義】
S, T を R の空集合ではない部分集合とする。
次の [1], [2] をともに満たすとき、{S, T} を R のデデキント切断という。
[1] S ∪ T = R
[2] ∀s∈S, ∀t∈T に対して、s < t
[2] で使った∀は「任意の」という論理記号です。どんな S の元と、どんな T の元で大小関係を比べても、T の元の方が S の元よりも大きいということになります。
また、この定義から、S と T の共通部分が空集合となっていることが分かります。
実際、{S, T} というデデキント切断について、
a∈S ∩ T が存在したとすると、次のような矛盾が生じます。
a∈S, a∈T なので、
[2] から a < a となります。
実数全体 R には順序の公理系も無条件で認められていて、議論をするときの下支えをしています。
そのため、高校の数学で学習した不等式の性質の通りです。
a < a ということは矛盾となります。
そのため、{S, T} が R のデデキント切断であるとき、S と T の共通部分は空集合となっています。
二つの実数 x と y について、「x < y または x = y または x > y」のいずれか 1 つのみが成立するというのが順序の公理の一つです。
a = a なので、a < a はダブルスタンダードとなってしまい、順序の公理に矛盾となるわけです。
岩井の数学ブログというサイトでは、ワイエルシュトラスの上限公理を実数の連続性の公理として、議論を始めています。
この記事では、そのワイエルシュトラスの上限公理とデデキントの切断公理が同値となっていることを示します。
それでは、このデデキント切断の定義に当てはまる具体例を見てみます。
デデキント切断の具体例
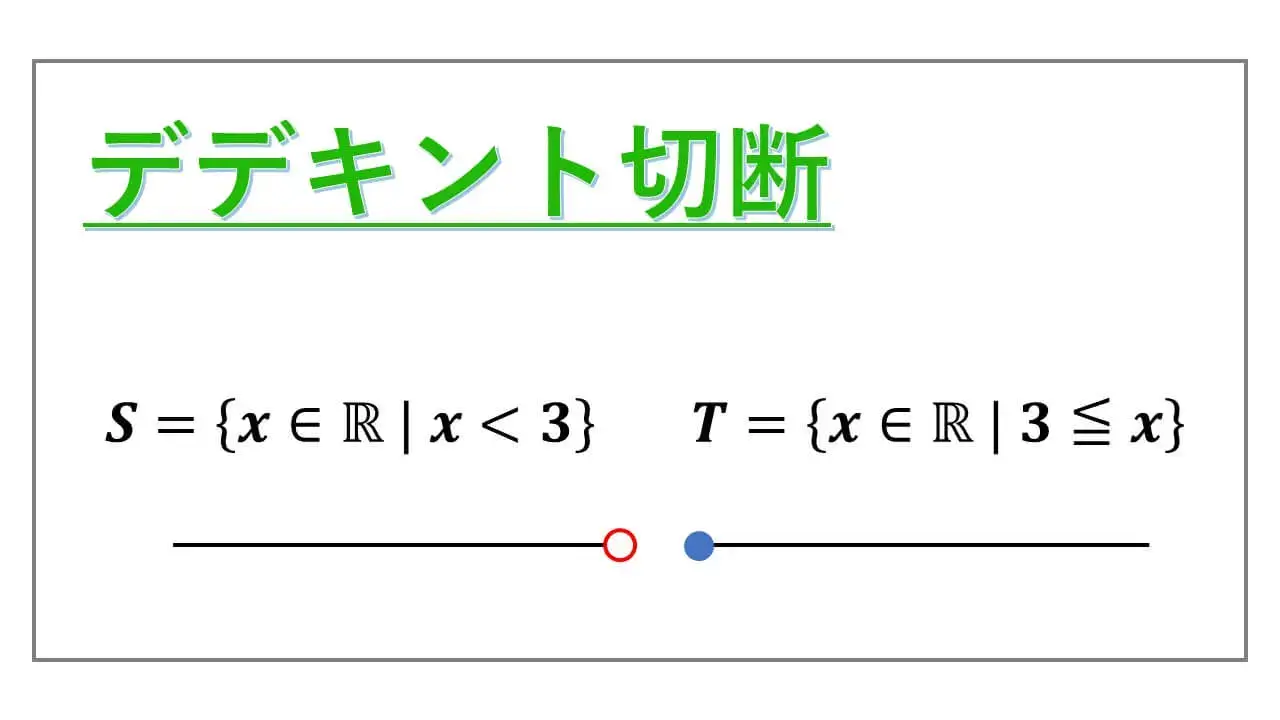
S = {x∈R | x < 3} という空集合でない R の部分集合を考えます。
そして、T = {x∈R | 3 ≦ x} とします。
r を実数とすると、順序の公理から、
r < 3 または r = 3 または r > 3 のいずれか 1 つのみが成立します。
そのため、r < 3 の場合は、r∈S です。
r = 3 または r > 3 の場合は、r∈T です。
よって、順序の公理から、
S ∪ T = R となっています。
これで、デデキント切断の定義 [1] を満たすことが確認できました。
次に、s∈S, t∈T を任意に取ります。
すると、s < 3 かつ 3 ≦ t となっています。
3 = t の場合は、
s < 3 =t なので、s < t です。
3 < t の場合は、
s < 3 かつ 3 < t なので、
順序の公理の一つである推移律から、
s < t となります。
これで、デデキント切断の [2] も確認できました。
以上から、{S, T} は R のデデキント切断となっています。
認められている公理と数学の推論規則から正しい命題を導きます。
ここまでは、順序の公理系が目立っていますが、ここからはワイエルシュトラスの上限公理が強力な下支えとなってくれます。
デデキント切断 :上界と上限についての認識を準備
A を R の空集合ではない集合とします。
r∈R が、任意の a∈A に対し、
a ≦ r を満たすとき、r を A の上界といいます。
この上界の定義から、r が A の上界ではないとすると、論理記号の否定を考えると、次のようになります。
つまり、「ある実数 a∈A が存在して、
a > r となる」ということです。
もう一つ、論理を用いて、シンプルな事実を導きます。
r∈R が空集合ではない R の部分集合 S の上界だとします。
このとき、x∈R が r < x となっていれば、x は S の元ではありません。
これは、背理法から導かれます。
もし x∈S とすると、r が S の上界であることから、
任意の s∈S に対して、s ≦ r となります。
x∈S だと仮定したので、s として x を考えると、
x ≦ r ということです。
今、r < x という設定の下で議論をしているので、
x ≦ r は順序の公理に矛盾します。
よって、背理法から、x は S の元ではないということになります。
もう一つ定義から明らかな内容を述べておきます。
A, B を R の空集合ではない部分集合とし、
A ⊂ B となっていたとします。
r∈R が B の上界となっているとき、r は T の上界にもなっています。
T の上界の定義を確かめます。
t∈T を任意に取ります。
すると、t∈A ⊂ B より、t∈B だから、
r が B の上界であるため、
t ≦ r です。
よって、T の上界の定義を r が満たすため、r は T の上界です。
それでは、次に上限についての内容を説明します。いよいよワイエルシュトラスの上限公理の出番です。
上限についての基本を理解する
S ⊂ R が空集合ではないとします。
このとき、X = {x∈R | x は S の上界} とします。
X に最小元(最小値)が存在したときに、その最小元を S の上限といいます。
S によっては、X に最小元が存在しないということもあります。もっというと、X が空集合となっているときもあります。
例えば、S = {a∈R | 3 < x} とすると、
S の上界は存在しません。
ここで、上に有界ということの定義を述べておきます。
【上に有界ということの定義】
S ⊂ R が空集合ではないとする。
S に上界が存在するとき、S は上に有界であるという。
S が上に有界だと、S の上界が少なくとも一つは存在するということです。
すると、X = {x∈R | x は S の上界} は空集合ではないということになります。
しかし、これだけでは X に最小元(最小値)が存在するかどうかは不明です。
ここで、ワイエルシュトラスの上限公理の出番です。
S が上に有界であるとき、
X = {x∈R | x は S の上界} に最小元(最小値)が存在するということを無条件で認めるという公理です。
この X の最小元のことを S の上限といいます。
sup S が S の上限を表す記号です。
ちなみに、最小元の定義は次です:
r∈R が r∈S を満たしかつ、
任意の s∈S に対して r ≦ s となっているとき、
r を S の最小元(最小値)といいます。
min S が、S の最小元を表す記号です。
※ max-min という記事で、最大値と最小値について高校内容から解説をしています。
このワイエルシュトラスの上限公理を実数の連続性の公理として、この数学サイトでは議論を進めています。
この記事では、デデキントの切断公理と同値となっていることを証明することを目指します。
では、S の上限と S の最大値についての命題を一つ示します。
最大元の定義も述べておきます。
r∈R が r∈S を満たしかつ、
任意の s∈S に対して s ≦ r となっているとき、
r を S の最大元(最大値)といいます。
max S が、S の最大元を表す記号です。
最大元と上限について
【命題1】
S ⊂ R を空集合ではないとし、S が上に有界であるとする。
このとき、max S が存在するとき、
max S = sup S となる。
<証明>
仮定より、ワイエルシュトラスの上限公理から、S には上限が存在します。
S の上限は、S の上界なので、
任意の s∈S に対して、
s ≦ sup S … (1)
また、仮定より、max S が存在しています。
max S ∈ S より、(1) の s として、
max S を考えると、
max S ≦ sup S … (2)
また、最大元の定義から、
任意の a∈S に対して、
a ≦ max S です。
そのため、max S は S の上界となっています。
つまり、
max S ∈ {x∈R | x は S の上界}
S の上限は、{x∈R | x は S の上界} の最小元なので、
sup S ≦ max S … (3)
(2), (3) より、順序の公理から、
max S = sup S 【証明完了】
それでは、ワイエルシュトラスの上限公理から、次のデデキントの切断公理を導きます。
ここまで述べてきた上界や上限についての理解があると、すぐに導けます。
デデキント切断 :ワイエルシュトラスから導く

<証明>
デデキント切断の定義 [2] から、
T の元は、すべて S の上界となっています。
T は空集合ではないので、S の上界が存在することから、S は上に有界です。
そのため、ワイエルシュトラスの上限公理から、S の上限が存在します。
論理的に、sup S という実数は、S に含まれていない場合と、S に含まれる場合に分かれます。
【sup S ∈ S の場合】
上限は S の上界なので、任意の s∈S に対して、
s ≦ sup S となります。
今、sup S ∈ S なので、sup S が S の最大元となっています。
そのため、この場合は、sup S が S の最大値です。よって、結論が導けました。
【sup S が S の元でない場合】
デデキント切断の定義の [1] から、
sup S ∈ R = S ∪ T です。
今、sup S は S の元ではないので、
sup S ∈ T … (3)
T の任意の元は、S の上界となっているので、
sup S ∈ {x∈R | x は S の上界}
かつ T ⊂ {x∈R | x は S の上界} となっています。
{x∈R | x は S の上界} の最小元が S の上限なので、
任意の t∈T に対して、
sup S ≦ t … (4)
(3), (4) より、
sup S という実数は、T の最小元の定義を満たしています。
よって、min T = sup S です。
これで、結論が導けました。【証明完了】
これで、デデキントの切断公理が導けました。さらに、論理的に、S の最大元と T の最小元が同時に存在しないということを示します。
境界点を含むのは片方のみ
【系】
{S, T} を R のデデキント切断とする。
このとき、max S と min T は同時に存在しない。
<証明>
背理法で示します。
max S と min T が両方とも存在したと仮定します。
max S ∈S, min T ∈T より、デデキントの切断の定義 [2] から、
max S < min T となります。
ここで、max S = a, min T = b と置きます。
(a+b)÷2 = c と置くと、
この実数 c は、a < c < b を満たします。
(実数体の公理から、加法と乗法から 2-1 を用いての除法)
実際、
c-a = b/2-a/2 = 1/2 × (b-a)
(実数体の公理の一つの分配律です。)
a < b より、
c-a = 1/2 × (b-a) > 0 となり、
a < c です。
また、b-c = 1/2(b-a) > 0 より、
c < b となっています。
今、max S = a < c だから、c は S に含まれていません。
そして、c < min S だから、c は T に含まれていません。
しかし、c∈R なので、デデキント切断の定義 [1] から、
c∈R = S ∪ T となっています。
そのため、c は S または T に含まれているため、矛盾です。
よって、背理法より、
max S と min T は両方とも存在しません。【証明完了】
順序の公理から、高校一年か二年のときに扱う不等式の証明の要領で、平均値を使って矛盾を見つけました。
両方とも同時に存在しないということと、【定理1】から、max S が存在するときには min T が存在せず、min T が存在するときには、max S が存在しないということになります。
では、【定理1】のデデキントの切断公理を認めると、ワイエルシュトラスの上限公理が導かれることを示します。
デデキント切断 :逆にワイエルシュトラスを導く
【定理2】
S を R の空集合ではない部分集合とする。
このとき、S が上に有界であるならば、S の上限が存在する。
デデキントの切断公理を認めているという前提で、ワイエルシュトラスの上限公理を導きます。
<証明>
仮定より、S が上に有界なので、
X = {x∈R | x は S の上界} は空集合ではありません。
ここで、max X が存在する場合と、存在しない場合に分かれます。
【max S が存在する場合】
最大元の定義から、max S ∈X です。
x∈X を任意に取ります。
x < max S とすると、
max S ∈ S なので、x が S の上界であることに反します。
そのため、順序の公理から、
max S ≦ x となります。
ゆえに、max S は X の最小元となっています。
よって、上界全体から成る集合 X の最小元である S の上限が存在することが示せました。
【max S が存在しない場合】
A = R-X と置きます。この差集合 A は R における X の補集合です。
実数 r について、S の上界となっているか、S の上界となっていないかなので、r は X に含まれるか、そうでなければ X に含まれないということになります。
よって、R = (R-X) ∪ X = A ∪ X です。
a∈A=R-X を任意に取ると、a は S の上界ではありません。
上界でないことから、ある S の元 b が存在して、
a < b となります。
今、S に最大元が存在しないことから、S の上界である X の元は、S に含まれません。
(S の上界が S に含まれると、その上界が S の最大元となるからです。)
そのため、S ⊂ R-X = A となっています。
ゆえに、c∈X を任意に取ると、c は S の上界だから、
b ≦ c ですが、c は S に含まれません。
そのため、b < c となります。
a < b かつ b < c なので、
a < c となります。
これで、A = R-X と X という空集合ではない R の部分集合は、R のデデキント切断の定義を満たしています。
{A, X} が R のデデキント切断なので、【定理1】から、
max A または min X が存在します。
max A が存在したとすると、
S ⊂ R-X = A だったから、
max A が S の上界となります。
しかし、max A ∈A = R-X なので、
max A は S の上界ではありません。
これは矛盾なので、max A が存在しないことになります。
よって、min X が存在しなければなりません。
この min X が、S の上界全体 X の最小元なので、
min X = sup S が存在します。【証明完了】
デデキントの切断公理(定理1)を認めると、論理パズルでワイエルシュトラスの上限公理が導かれます。
これで、ワイエルシュトラスの上限公理とデデキントの切断公理が同値であることを示すことができました。
数学における推論規則の下で、実数全体から成る集合 R は、実数体の公理と順序の公理を満たすもので、さらに実数の連続性の公理を満たすものという前提で、微分積分学の理論が作られています。
同値なので、ワイエルシュトラスの上限公理を連続性の公理として採用したら、デデキントの切断公理(定理1)も認めたことになります。
逆に、デデキントの切断公理を実数の連続性の公理として採用したら、ワイエルシュトラスの上限公理も認めたことになります。
この二つは、論理パズルで同値であることが示せるので、他の公理との同値であることの証明の中では、比較的に同値であることを確認しやすいものかと思います。
また、集合と論理規則を使っての証明に触れることができるので、集合論入門や位相空間の入門の前の良いトレーニングにもなるかと思います。
論理記号については、別の記事で解説をしています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。