アルキメデスの原理 – 浮力の原理 | 浮力について分かりやすく解説
" アルキメデスの原理 (浮力の原理) “をできるだけ簡単な言葉や数字を用いて解説しています。
中学の理科や数学で扱う内容で、シンプルな例を用いて浮力の計算について学習をし始めると良いかと思います。
単位を置き換えたりする内容が絡むときもありますが、算数の頃に学習した親しみやすい単位を中心にして話を進めています。
密度や体積についての単位を書き直すことも含めると複雑になってくるので、あくまで基礎的な公式の使い方に軸足を置いています。
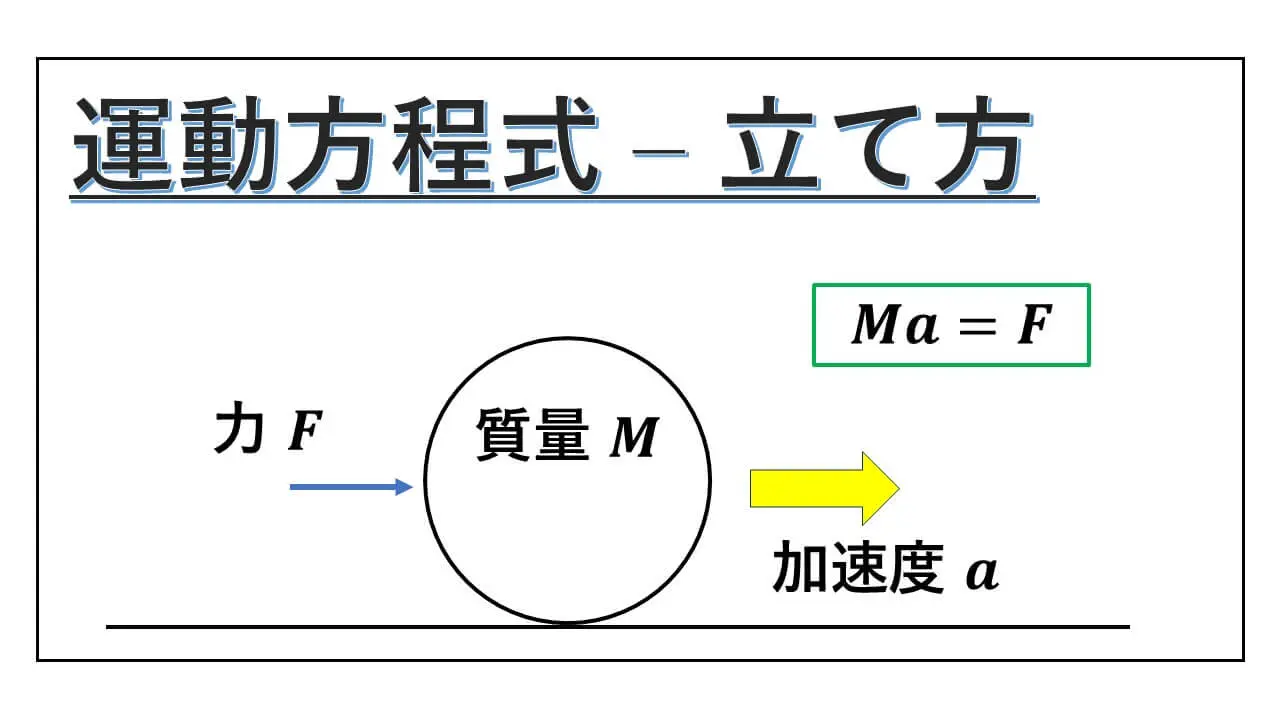
アルキメデスの原理 – 浮力の原理
静止した物体が受ける、排除した流体の重量に等しい上向きの力が浮力である。
高校の物理などでは、このような感じに難しい言葉で浮力が述べられます。
そこで、より分かりやすい言葉で浮力について説明をするようにします。
浮力という力は、密度と体積に関連して定まります。
その内容をシンプルに述べると次のようになります。
【浮力】
液体の密度×おしのけた液体の体積
水などの液体に物体をつけたときに、水面の下に浸かった物体の体積を用いて計算されます。
中学の理科などで出題される問題では、単位を書き換えることも含めた問題が出され、そのせいでややこしくなります。
そこで、算数で学習した身近な単位を使って話を進めることにします。
g/cm3を液体の密度とし、体積も cm3 だけを使って説明をすることにします。
力の大きさを表す単位として、100 g を 1 N とする単位もありますが、g のままで算数のように扱うことにします。
ばねばかりなどで力の大きさを測った通り、5 g の力がかかっているというように気楽に述べることにします。
では具体的な数字を使って、練習してみます。
練習問題1
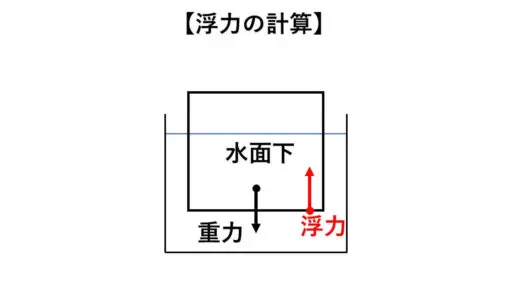
図のように物体が水面上に静止しているとします。
1g/cm3を水の密度とします。
この物体の重さを 150 g とし、水面下に沈んでいる部分の体積が何 cm3となっているのかを求めてください。
<解答と解説>
求める物体の体積を a cm3として、文字 a の値を求めます。
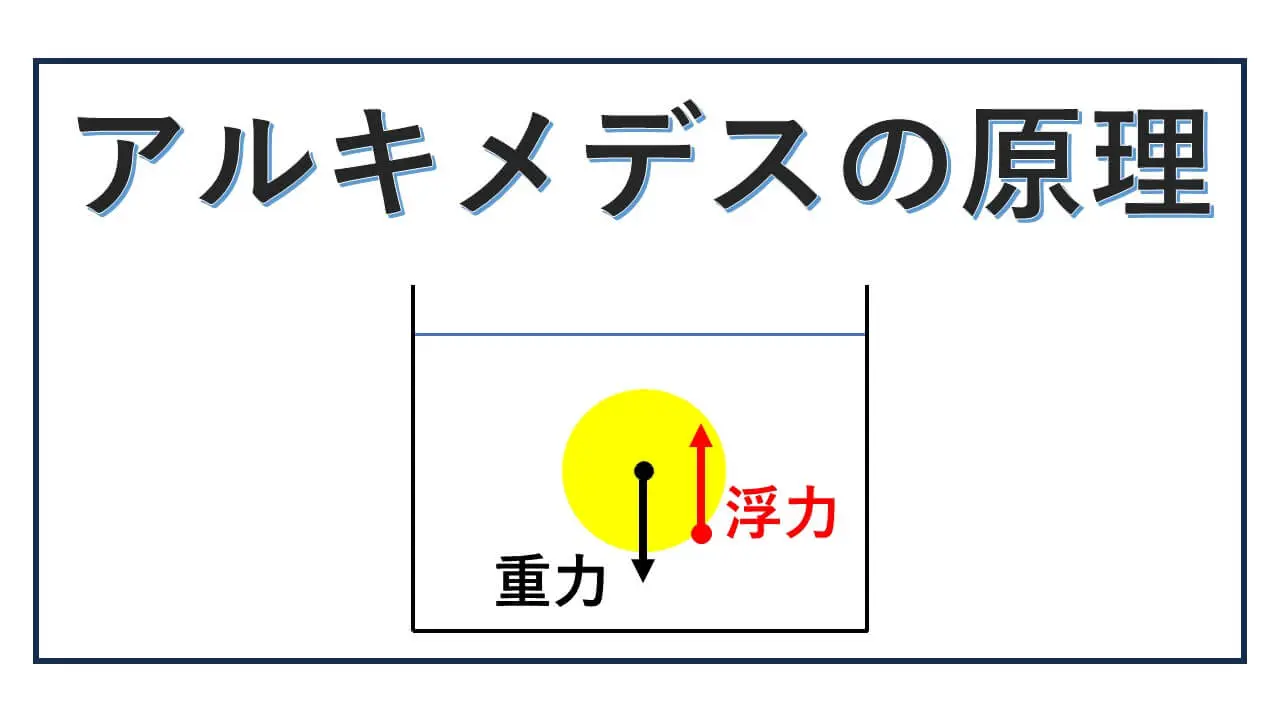
重力という物体が地球の中心に向かって引かれる下向きの力は物体の重さに等しいです。
そのため、150 g が重力による下向きに物体が引かれる力の大きさになります。
物体が水面上に静止しているということから、下向きの重力の大きさと上向きの力である浮力が同じ大きさになっていると考えます。
そのため、150 g が浮力の大きさです。
ここで、アルキメデスの原理(浮力の原理)の式で、浮力の大きさを文字 a を用いて表します。
液体の密度×おしのけた液体の体積 が浮力でした。
今、液体である水の密度は、1g/cm3です。
おしのけた水の体積は、求める水に沈んでいる部分の物体の体積 a cm3です。
以上より、
1 × a = 150 です。
つまり、a = 150 で、
150 cm3が求める体積ということになります。
g/cm3 に cm3 を掛けると、単位の分母が約分されて g が単位となります。
先ほど、
1[g/cm3] × a [cm3]
= 150 [g] という計算を浮力の大きさを表す単位を g で計算しました。
ここまでの内容に慣れると、さらに g を N の単位に置き換えることもできます。
g を 100 で割ると N の単位に変換することができます。
150÷100 より、
150 g は 1.5 N ということになります。
今度は水と異なる液体で同じように浮力の計算をしてみます。
練習問題2
先ほどの図と同じように物体がサラダ油の上に静止しているとします。
0.7 g/cm3をサラダ油の密度とします。
この物体の重さを 140 g とし、水面下に沈んでいる部分の体積が何 cm3となっているのかを求めてください。
<解答と解説>
今度はサラダ油で密度の値が変わりました。
求める物体の体積を a cm3として、文字 a の値を求めます。
重力という物体が地球の中心に向かって引かれる下向きの力は物体の重さに等しいです。
そのため、140 g が重力による下向きに物体が引かれる力の大きさになります。
物体がサラダ油の上に静止しているということから、下向きの重力の大きさと上向きの力である浮力が同じ大きさになっていると考えます。
そのため、140 g が浮力の大きさです。
液体の密度×おしのけた液体の体積 が浮力 140 g なので等式が得られます。
0.7 × a = 140 です。
よって、
a = 140÷0.7
= 200 [cm3] となります。
200 cm3が求める体積ということになります。
浮力を求める式に使われている密度という単位について、もう少し詳しく説明をしておきます。
密度という単位について
密度を表す単位を中学の理科で、g/cm3と習います。
グラム毎立法センチメートルと読みます。
この密度という数字は、1cm3の体積あたりの質量を表しています。
密度は物質によって、その値が決まっています。
鉄の缶とアルミ缶の体積が同じであったとしても、質量を測ると異なるといったものです。
密度について、水は 1g/cm3 ということを知識として知っておくと良いかと思います。
※ 中学校の理科のテストで水の密度が問われることもあります。
鉄の缶の密度は 1g/cm3よりも大きい値なので、鉄は水に沈みます。
鉄の密度は約 8 g/cm3くらいです。
そのせいで、上向きの浮力よりも下向きに移動する力の方が大きくなって鉄が沈むということを小学校の理科などで経験しています。
発泡スチロールのように水よりも密度が小さい物質が水に浮くということも経験しています。
厳密な数字を使っていない経験ですが、高校の物理などになると文字を使いながら力の方向や大きさを意識して計算を進めたりします。
密度については、算数の単位あたりの数量の考え方で計算ができるので、中学一年生の段階から押さえることができます。
少し練習してみます。
浮力計算のためにも密度の練習
体積 25cm3 の質量が 75 g の物質があったとします。
この物質の密度を求めてください。
1cm3 あたりの質量が密度なので、単位あたりの量の考え方で計算できます。
75 g を 25 等分したうちの1つという考え方をします。
75 ÷ 25 = 3 より、
3cm3 が求める密度です。
算数で学習した単位あたりの量の内容を突き詰めると比の内容なので、比を使っても計算することができます。
1cm3 あたりの質量が a g だとして、
75 : 25 = a : 1 という関係になります。
そのため、25a = 75 なので、
a = 75÷25 = 3 [cm3] となります。
先ほど、この割り算を単位あたりの量の考え方で計算していたというわけです。
割られる数と割る数と商の関係からも、密度の式を書き換えることも大切になります。
商に割る数を掛けると割られる数になるという書き換えです。
質量[g]÷体積[cm3]
=密度[g/cm3]だから、
密度[g/cm3]×体積[cm3]
=質量[g] となります。
例えば、密度 3 cm3の物体の体積が 25 cm3 だと、この物体の質量を計算することができます。
3 × 25 = 75 [g] ということになります。
このように、既に算数や中学の数学で学習した計算のきまりに基づいて、理科の計算を進めることができます。
ちなみに、アルキメデスですが、大学の数学科でもアルキメデスの性質という難しい内容が出てきます。
あくまで参考程度に、その内容を少し述べておきます。
参考までに大学の内容
この記事では、実数全体から成る集合を R、自然数全体から成る集合を N と表すことにします。まず、上界と上限の定義を押さえておきます。
【上界の定義】
S ⊂ R が空集合でないとする。
実数 r が、∀s∈S に対して、
s ≦ r となるとき、r を部分集合 S の上界といいます。
【上限の定義】
S ⊂ R が空集合でないとする。
{r∈R | r は S の上界} に最小値が存在するとき、その最小値を S の上限という。
S の上限が存在するとき、
sup S で、S の上界を表す。
実数 r が S の上界であることの定義は、S のどの元 s に対しても、s ≦ r となっているということです。
上界や上限については、存在しないときもあるので注意です。
例えば、{x∈R | 3 < x} という R の部分集合については、上界が存在しません。そのため、上界たちを集めた集合は空集合となり、上限も存在しません。
S = {x∈R | x < 3} だと、4 や 5 などが S の上界となります。
「S に上界が少なくとも 1 つ存在するとき、必ず S の上限となる実数が存在する」というのが、ワイエルシュトラスの上限公理です。
他にも同値なものが複数あって、どれか一つを実数の連続性の公理として採用し、議論を進めます。
この記事では、ワイエルシュトラスの上限公理を実数の連続性の公理としています。
そのため、S = {x∈R | x < 3} には、上限が存在します。
実は、アルキメデスの性質を証明しようとするときに、S に上限が含まれるかどうかの判断が大切になります。
上限を含むかどうか
S ⊂ R の上限 sup S が存在するときに、上限が S に含まれているかどうかは、S によって様々です。
【例】
S = {x∈R | x < 3} の上限は、3 となります。
sup S = 3 という実数は、S に含まれていません。
一方、T = {x∈R | x ≦ 3} だと、
sup T = 3 は T に含まれています。
こういった部分集合によって、その上限が存在したとしても、上限をその部分集合の中に含んでいるかどうかは、一概になんとも言えません。
アルキメデスの性質の証明は、上限を含むかどうかが不明な状況で論理的に推論を進めることになります。
あと用語ですが、S ⊂ R が空集合でないときに、S の上界が一つでも存在すると、S は上に有界といいます。
W = {x∈R | x2 < 3} だと、0∈W なので W は空集合ではありません。そした、7 は W の上界なので、W は上に有界ということになります。
それでは、ここまでの内容を踏まえて、アルキメデスの性質という命題の証明をします。
アルキメデスの性質
【定理】
自然数全体 N は上に有界ではない。
<証明>
N が上に有界だと仮定して、矛盾を導きます。
N が上に有界だと、ワイエルシュトラスの上限公理(実数の連続性の公理)から、N に上限が存在することになります。
r = sup N と置きます。
上限の最小性から、r-1 < r は N の上界ではありません。
これは、r-1 がN の上界だとすると、r-1 は r より小さい上界ということになり、r が N の上界全体の中で最小であったことに反するからです。
論理的に、r-1 が N の上界ではないということが分かりました。
そうすると、上界であるということの否定が使えます。
実数 x が、∀s∈S に対して、
s ≦ x となるとき、x を S の上界と定義しました。
今、r-1 は S の上界ではないので、この否定が成立します。
すなわち、
∃n∈N such that " n > r-1 “
ここまでの状況から、矛盾を探します。
矛盾を見つけて背理法
今、自然数 n は、n > r-1 を満たしています。
n は自然数なので、n+1 は n より大きい自然数です。
そのため、
N∋n+1 > (r-1)+1 = r
r = sup N だったので、N の上界です。
上界の定義から、どの自然数 k に対しても、
k ≦ r です。
k として、n+1 を考えると、
n+1 ≦ r です。
n+1 ≦ r と n+1 > r が両方とも成立することになりました。まさに矛盾です。
よって、背理法から、
自然数全体 N が上に有界ではないということになります。【証明完了】
ワイエルシュトラスの上限公理によって、上限の存在が示されたことで、背理法による証明が可能となりました。
この証明した【定理】を使って、塵も積もれば山となるで有名なアルキメデスの性質を導きます。
高校の数学で学習した不等式の性質も、順序の公理として認められていますので、それを使います。
では、数学について、よく知られた内容を厳密に証明します。
塵も積もれば山となることを証明
【アルキメデスの性質(定理)】
任意の正の実数 ε, a が与えられたとする。
このとき、ある自然数 n が存在して
ε ≦ n × a となる。
<証明>
任意に正の実数 ε, a が与えられたとします。
どちらも正の実数なので、
ε÷a も正の実数です。
先ほど示した【定理】から、
ε÷a は、自然数全体 N の上界ではありません。
そのため、ある自然数 n が存在した、
ε÷a ≦ n となります。
両辺に正の実数 a を掛けても不等号の向きは、そのままです。
よって、ε ≦ n×a 【証明完了】
このアルキメデスの性質を利用して、高校で学習する数列の極限で認めていたことが証明されることになります。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。