一意 【一意性の証明】| 後半で大学で扱う極限の一意性も
一意 (uniqueness) という言葉は、大学数学を学習しているとよく出てきます。
微分積分学や線形代数学の本を見ると、一意的である (unique, uniquely) と、よく書かれています。
ユニークであるということの定義を知った上で、一意性をどう証明するのか。大学数学の内容を理解する上で、基本となる大切な内容になります。
大学で使うような数学の本を見ると「一意である」ということが、とてもよく書かれています。そのため、早い段階で押さえておくと良いかと思います。
「一意 (uniqueness) 」ということを使いこなせるようになるためには、シンプルな具体的な例を通して理解しておくと良いかと思います。
シンプルな具体例だけれども、あらゆるタイプの一意性の証明の方針が分かるようなものを早い段階で経験しておくと、大学数学を学習するときに、勉強がしやすくなります。
一意という言葉は、ただ一つである、ただ一通りであるという意味です。このことを数学の証明において、どのように扱えば良いのかということを押さえておくのが大切になるかと思います。
一意である、つまり、唯一であるという意味を押さえると、気になるのは、どうやって一意性を証明するのかということになります。
数学において、一意性を証明するには型があるので、その大枠を知ることからスタートします。
一意 unique :一意であることの証明の方針
条件を満たすものが一意的に存在するということの証明方針は、大きく次の二通りです。
一意であることを証明するときには、どちらの方針で証明を進めるのかをまず吟味すると良いかと思います。
① その条件を満たす異なるものが 2 つ存在したとして矛盾を導く。
② その条件を満たすものを任意に 2 つとってきて、その 2 つが一致していることを示す。
一意性の証明をするための代表的な型になります。
①の方針は、高校数学で学習する背理法です。異なる 2 つのものが条件を満たしたして、矛盾を導きます。
②の方針は、高校数学では、あまり馴染みがないかもしれません。しかし、大学数学についての本を読んだりすると、よく出てきます。
例えば、次のような内容が出てきます。
ベクトル空間 V の加法についての零元は 0 のみである。
ベクトル空間の公理より
「零元は 0 のみ」というのは、零元が 0 ただ一つということを意味しています。
唯一ということが一意でした。
大学の数学では、こういうときに、証明が必要になります。
そのときに、一意であることを証明するための型を押さえておくと、その型の通りになっているということを示すことができます。
証明方針②を使うと次のように示します。

このように、零元であるという条件を満たすものが、0 と x と二つあったら、どちらも一致するということを示すのが、証明方針の②です。
とはいえ、この方針を今のような抽象的な文章で初めて見ると、何を言っているのかイマイチ分かりにくいものかと思います。
このようなときに、具体例を通して様子を見ると理解が深まります。
以下で掘り下げて議論を深めていきます。
一意 unique :一意性の証明の具体例
実は、この一意性について、中学 1 年の数学で経験するようになっています。
ただ、中 1 の授業では、あまり深くは扱われないはずです。
方程式の解を学習するときに、実数係数の一元一次方程式の解がただ 1 つであるということが出てきます。
ちょうど、これを通して、先ほどの①と②の証明方針を確かめると、大学 1 年の数学の勉強の備えになります。
x を実数とする。
x についての方程式 2x = 6 の実数解が存在し、しかも、その解は一意的である。
中学 1 年の数学の内容を大学数学風に書いてみました。
この実数解は、x = 3 ですが、これ以外に実数解が存在しないということです。
今、分かっていることとして、2 × 3 = 6 なので、3 という実数解が存在しているということです。
この実数 3 しか、2x = 6 の実数解が存在しないということを証明したいわけです。
そんなときに、まずは方針①「 その条件を満たす異なるものが 2 つ存在したとして矛盾を導く」で、他に実数解が存在しないことを確かめてみます。
その後で、方針②でも確かめてみます。
※この例では、条件を満たすということは、x についての方程式の実数解であるということです。
方針①での一意性証明
もし、3 とは異なる実数 a が、2x = 6 の解だとします。解なので、方程式に代入したときに、2a = 6 となります。
両辺を 2 で割ると、a = 3 となります。
これは、a が 3 とは異なる実数であったことに矛盾します。
というわけで、2x = 6 の実数解が、3 以外には存在しないということが証明できました。
方針②での一意性証明
今度は、方針②「 その条件を満たすものを任意に 2 つとってきて、その 2 つが一致していることを示す 」を考えます。
実数 p と実数 q が 2x = 6 の解だとします。
すると、どちらも解なので、2p = 6 = 2q となります。
すなわち、2p = 2q
この両辺を 2 で割ると、p = q となります。
これで、2x = 6 の実数解が 2 つあったとすれば、どちらの実数解も等しいということが示せました。
3 は、直接計算 2 × 3 = 6 から、実数解であることが分かるので、実数 p として 3 を考えると、もう一方の実数 q は、必然的に 3 と等しいということになります。
これで、方針②でも、2x = 6 の実数解が 3 のみであることが証明できました。
実は、条件を満たすものの存在証明と、条件を満たすものが存在したとすると一意的であることの証明は、別の数学的な証明になります。
今回の例では、実数 3 が直接計算 2 × 3 = 6 から、実数解が少なくとも一つは存在すると分かっている状態から議論をはじめました。
実際に、大学数学を学習するときには、もっと複雑な状況が出てくると思います。そのときには、次の二つを区別することが大切になります。
- 条件を満たすものが存在することの証明をしているのか
- 存在したとすると一意的であることを証明するのか
一意 unique :微分積分風の具体例
二次関数 f(x) = x2 は、開区間 (-1, 1) において最小値をとる。
しかも、その最小値を与える定義域の元は一意である。
※最大値と最小値についての正確な定義については、max min というブログ記事で解説をしています。
あえて、大学数学風に当たり前のことを書いてみました。
二次関数のグラフである放物線については、グラフの概形を中学数学で学習しているので、グラフより x = 0 で最小値 f(0) = 0 なのですが、このことを証明してみます。
開区間 (-1, 1) というのは、
S = {x | x は -1 < x < 1 を満たす実数} です。
f(x) = x2 が開区間 (-1, 1) において、x = a で最小値をとるということを正確に表現します。
「この範囲内に含まれている実数 a で、どんな x ∈ S に対しても f(a) ≦ f(x) となる」ということです。
まず、最小値が存在することを証明します。
f(0) = 02 = 0 です。実数 b が -1 ≦ b < 0 であるとき、f(b) = b2 > 0 となります。
そして、実数 b が 0 < b ≦ 1 であるとき、f(b) = b2 > 0 となります。
これで、開区間 (-1, 1) に含まれているすべての実数について調べたことから、実数 x が -1 < x < 1 のとき、f(0) ≦ f(x) ということが示せました。
すなわち、x = 0 において最小値をとることが示せました。
最小値を与える開区間 (-1, 1) 内の実数が存在することが証明できたということになります。
存在証明の後に、確認したいのが、一意性の証明です。
ただ、先ほどの議論から、既に一意性の証明は明らかになっています。ここをていねいに見ていきます。
方針①の背理法で一意性を確認します。
もし、0 とは異なる開区間 (-1, 1) に含まれる実数 p において、f(x) が最小値をとったとします。
すると、最小値の定義から、f(p) ≦ f(0) です。
一方、x = 0 において最小値をとることは先ほど確認しましたから、f(0) ≦ f(p) です。
f(p) ≦ f(0) かつ f(0) ≦ f(p) なので、f(p) = f(0) = 0 です。しかし、p は、 0 とは異なる開区間 (-1, 1) に含まれる実数 でした。
-1 < p < 0 または 0 < p < 1 です。
どちらの場合も、f(p) = p2 > 0 となります。これは、f(p) = 0 であることに矛盾します。
したがって、 開区間 (-1, 1) において、最小値をとるのは、x = 0 のときしかないということです。
前提となる範囲内で考える
数学で、条件を満たすものが存在することを存在証明。存在したとすると一意的でことの証明を一意性の証明ということを述べてきました。
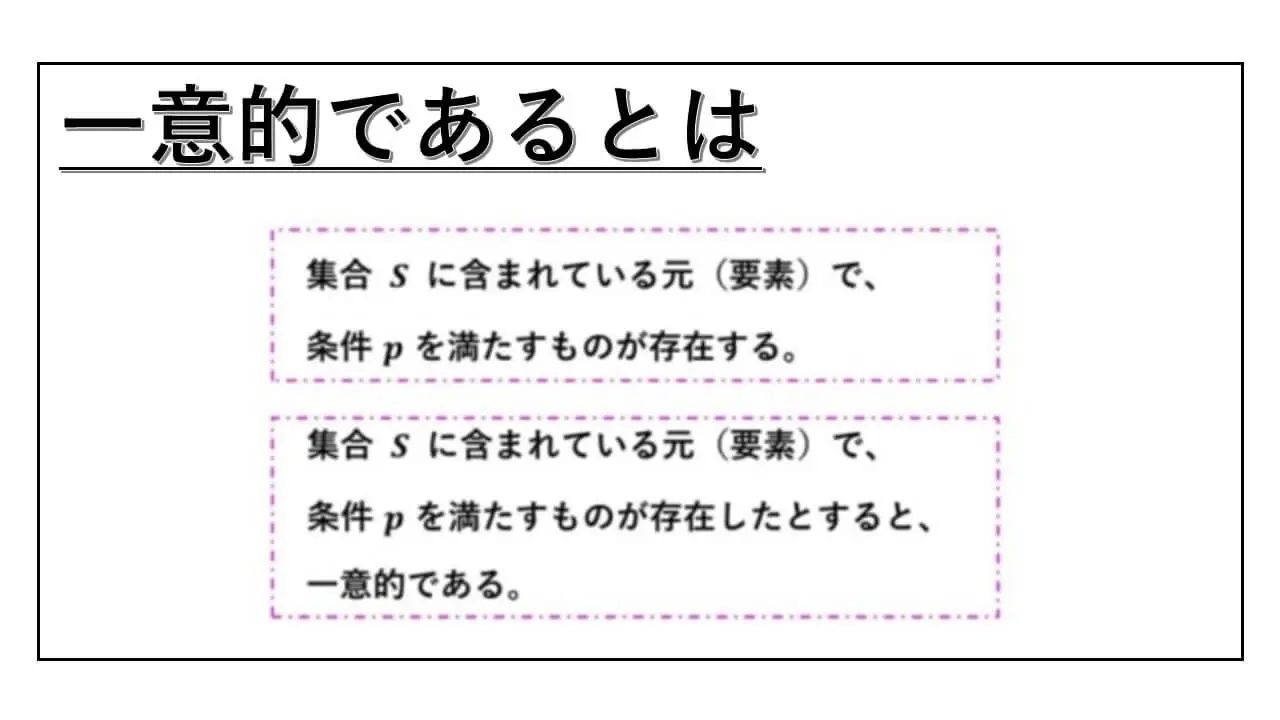
ここで、注意点ですが、存在証明にせよ、一意性の証明にせよ、条件を満たすかどうかを考えるときに、対象となる集合の範囲を明確にしておく必要があります。
・集合 S に含まれている元(要素)で、条件 p を満たすものが存在する。
・集合 S に含まれている元(要素)で、条件 p を満たすものが存在したとすると、それは一意的である。
このように、条件を満たすものかどうかを議論するときには、どの集合の範囲内で考えているかということを明確にしておく必要があります。
集合 S と書いているのですが、この S がある集合のときには、条件を満たすものが存在したが、ちがう集合 S’で考えると、条件を満たすものが存在しないということも起きてきます。
先ほどの二次関数 f(x) = x2 では、
S = { x | x は -1 < x < 1 である実数 } という開区間 (-1, 1) の範囲内の実数を対象として、最小値が存在するということを議論しました。
この S を、{ x | x は 2 < x である実数 } という範囲で考えると、最小値は存在しません。このように、対象となる集合を変えると、存在するかどうかが変わることも起こり得ます。
一意性についても、狭い範囲では一意的だったけれども、より広い範囲で考えると、異なるもので条件を満たすものが出てきたということが起こり得ます。
一般的に、想定外の出来事ということです。数学でも、条件を満たすものについて議論をするときには、例外が出ると反例となり、命題が偽となるので、注意が必要になります。
先ほどの f(x) = x2 は、{ x | x は 2 < x である実数 } という範囲で考えると、最小値は存在しませんでした。連続関数ですが、{ x | x は 2 < x である実数 } が有界閉集合ではありません。
このように、数学の真である定理は、条件を満たすものについては、必ず結論を満たしますが、条件を満たさないものについては、定かではありません。
ここからの後半部分では、数学科で扱う極限の一意性を証明します。
数列が収束するときに、その収束する値はただ1つであるということの証明になります。
実数全体を R として議論を進めています。
極限の一意性を証明
【極限の唯一性】
s と t を実数とする。
実数列 {an} に関し、
ある自然数 N1 が存在し、
N1 ≦ n である任意の自然数 n に対して、
「0 < ε を満たす任意の ε∈R について
|an-s| < ε 」が成立するとする。
また、
ある自然数 N2 が存在し、
N2 ≦ n である任意の自然数 n に対して、
「0 < ε を満たす任意の ε∈R について
|an-t| < ε 」が成立するとする。
このとき、s = t である。
<証明>
0 < ε を満たす任意の ε∈R が与えられたとします。
すると、
0 < 2-1・ε です。
仮定より、
ある自然数 N1 が存在し、
N1 ≦ n である任意の自然数 n に対して、
|an-s| < 2-1・ε です。
同様に、
ある自然数 N2 が存在し、
N2 ≦ n である任意の自然数 n に対して、
|an-t| < 2-1・ε です。
N = max{N1, N2} と置きます。
すると、N ≦ n を満たす自然数 n に対して、
|an-s| < 2-1・ε,
|an-s| < 2-1・ε
よって、
|s-t| = |s-an+an-t|
≦ |s-an|+|an-t|
= |an-s|+|an-t|
< 2-1・ε+2-1・ε
= (2-1+2-1)・ε = ε
即ち、0 < ε を満たす任意の ε∈R に対して、
|s-t| < ε となっています。
よって、
s = t です。【証明完了】
証明した定理は、数列が収束するときは必ず同じ値に収束するということを保証します。
証明の最後の部分で s と t が一致するとしたことのより厳密な背景となる命題も述べておきます。
補足となる内容
【命題1】
x∈R が、0 ≦ x だとする。
そして、
「r > 0 を満たす任意の r∈R に対し
x < r である」とする。
このとき、x = 0 である。
0 < x だとし、矛盾を導きます。
0 < x = 2x-x です。
0 < 2x-x の両辺に x を加え
x < 2x を得ます。
また、0 < 1 より
0 < 2 が導けます。
すると、
0 < 2-1 を得ます。
よって、
0 < x と x < 2x に、2-1 を両辺に掛けます。
すると、
0 < 2-1・x と 2-1・x < x を得ます。
r = 2-1・x と置くと、
r∈R は 0 < r となっています。
よって、仮定から、
x < r です。
r を元に戻すと、
x < 2-1・x です。
しかし、今、
2-1・x < x です。
これは、< についての順序の公理に矛盾します。
そのため、背理法から、
x = 0 となります。【証明完了】
この【命題1】と絶対値を合わせると、数列の極限についての内容に関連する命題が導けます。
a∈R について、
0 ≦ a のとき |a| = a,
a < 0 のとき |a| = -a というのが絶対値の定義です。
さらに、次の命題を示します。
この【命題2】が、先ほどの極限の一意性の証明の最後で使った内容になります。
【命題2】
a, b∈R とする。
そして、
0 < ε を満たす任意の ε∈R に対して、
|a-b| < ε となっていたとする。
このとき、a = b である。
<証明>
x = |a-b| と置きます。
すると、0 ≦ x です。
この x について、
0 < ε を満たす任意の ε∈R に対して、
x < ε となっています。
そのため、【命題1】を適用することができます。
よって、x = 0 です。
つまり、|a-b| = 0 です。
0 < a-b とすると、
a-b = |a-b| = 0 より、
a = b となり、
a-b = 0 かつ 0 < a-b という矛盾が生じます。
a-b < 0 とすると、
-(a-b) = |a-b| = 0 より、
a = b となり、
a-b = 0 かつ a-b < 0 という矛盾が生じます。
ゆえに、a = b です。【証明完了】
一意性の証明は、様々な分野で出てくるので、慣れておくと良いかと思います。
極限の大学での内容として、イプシロンデルタ論法という記事も投稿しています。
それでは、これで、このブログ記事を終了します。
読んで頂き、ありがとうございました。