連続関数 ; 最大・最小値の存在を示す定理【n次元の有界閉領域まで】
実数値をとる「 連続関数 」についての最大値・最小値の存在を示す定理の証明を書いています。
「 有界閉区間 」上で定義された連続関数がその値域において最大値と最小値をとるという定理の証明です。
そして、n 次元のユークリッド空間へ拡張された定理の証明になります。大学数学の微分積分学を学習するときに、基本となる定理の一つになります。
高校数学では厳密な証明を通常は扱わないだけに、大学数学を学習するときに、厄介な壁となります。
私が高校生の時に「大学で証明を学習するから」と授業で聞き、いざ大学の微分積分学の講義を受けていると、いつの間にか「既に述べたことより明らか」と分からないまま終了していました。
こういった経験から、このブログが少しでも読者の方の理解の助けになれれば幸いです。
なお、今回の定理の証明では、実数の連続性の公理として「有界な数列は収束する部分列をもつ」ということを使います。
ちなみに、「上に有界な実数の集合は上限をもつ」、もしくは、「下に有界な実数の集合は下限をもつ」といのが実数の連続性の公理です。
そして、これは、次の 4 つと必要十分条件になります。
1. 有界な数列は収束する部分列をもつ
2. コーシー列は収束する
3. 上に有界な単調非減少数列は収束する
4. 下に有界な単調非増加数列は収束する
この実数の連続性の公理が成立することを前提にして、大学数学の微分積分学（初等解析学）がスタートします。
連続関数 :定理の前の準備
このブログでの記号の使い方として、自然数全体から成る集合を N と表し、実数全体から成る集合については R と表しています。
そして、N から R への関数（写像）のことを数列と呼ぶことにします。
また、数列 a : N → R と、N から N への単調増加関数 φ について、合成関数 a・φ を数列 a の部分列といいます。
※単調増加関数とは、k < l ならば、φ(k) < φ(l)となる関数です。
数列 a の値域を {a(n) | n ∈ N} と表します。
関数の対応に注目して an よりも a(n) という記号を使っています。
この値域が有界であるときに、実数の連続性の公理を使うチャンスとなります。
部分列は合成関数なので、N → N → R という対応で、N から R への関数です。そのため、数列ということになります。
{a(φ(n)) | n ∈ N} が部分列の値域で、これは数列 a の値域の部分集合となっています。
記号で述べると、
{a(φ(n)) | n ∈ N} ⊂ {a(n) | n ∈ N} です。
また、実数 t について、実数 ε に対する 点 t を中心とする ε 近傍とは、
{x ∈ R | t － ε < x < t + ε} という集合のことです。
ε 近傍も、今回の証明で使います。
上界と下界
今回の証明したい定理に、有界という言葉があるので、有界ということについての定義を書いておきます。そのために、上界と下界という言葉を押さえる必要があります。
R の部分集合 S について、実数 x が S のどんな要素（元）s に対しても、s ≦ x となるとき、s を集合 S の上界といいます。
また、実数 y が S のどんな要素 s に対しても、y ≦ s となるとき、yを集合 S の下界といいます。
R の部分集合 S が、少なくとも 1 つ上界をもつとき、集合 S は上に有界といいます。
また、少なくとも 1 つ下界をもつとき、下に有界といいます。
上にも下にも有界なときは、単に有界といいます。これで、有界という言葉の定義が与えられました。
実は、1 次元ユークリッド空間について、閉区間は有界となります。
上限と下限
R の部分集合 S について、実数 x が S の上界であり、かつ t < x となる実数 t は必ず S の上界でないときに、この x を S の上限といいます。
S の上限のことを sup S と表します。
また、実数 y が S の下界であり、かつ y < tとなる実数は必ず S の下界でないときに、この y を S の下限といいます。
S の下限のことを inf S と表します。
連続関数 :有界閉区間上で定義された連続関数の定理
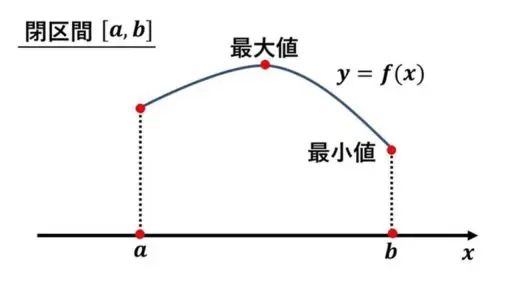
それでは、有界閉区間を定義域とする連続関数が、その値域において最大値と最小値をとることを証明します。
※ イプシロンデルタ論法というブログで連続の定義について説明をしています。
【定理】
有界閉区間 I = [a, b] 上で定義された連続関数 f は、値域 f(I) において最大値および最小値をもつ。
証明は、[1] の部分と [2] の部分に分かれます。
[1] で、閉区間 I の f による像 f(I) が有界であることを示します。
その後で、[2] で、値域 f(I) の中で最大値と最小値が存在することを示します。
[1] の部分の証明
[1] f(I) が有界であることをまず示します。
もし f(I) が有界でないと仮定すると、
「任意の自然数 n に対して、f(I) に上界が存在しないので、ある実数 x∈I が存在して、n < f(x) 」(★)となります。
自然数 n に対して、このような x の 1 つをとり、x(n) と定めます。
これで、自然数全体 N から I への数列 t が定義できました。
n ∈ N に対して、t(n) = x(n) と対応
* t(n) = x(n) は f の定義域である [a, b] = I 内の元
{t(n) | n∈N} は有界閉区間 I の部分集合だから、有界です。
よって、実数の連続性の公理より、収束する部分列が存在します。
この収束部分列を {t(φ(n)) | n ∈ N} と表すことにします。
そして、この部分列の収束する値を実数 p とします。
ここで、任意の自然数 n に対して、t(n) は I に含まれるので、t(n) ≦ b
※ t(n) ∈ [a, b] のため
そのため、部分列についても、t(φ(n)) ≦ b です。
したがって、収束値は、p ≦ b となります。
また、同様に考え、a ≦ p でもあるので、p は閉区間 I 内の点です。
仮定より、関数 f は I 内で連続だから、特に、点 p において連続です。
よって、任意の正の実数 r に対して、正の実数 δ(r) が存在して、x ∈ I かつ |x － p| < δ(r) ならば、|f(x) － f(p)| < ε
※イプシロンデルタ論法での連続の定義
正の実数 ε に対して、部分列が p に収束することから、ある自然数 k(ε) が存在して、n ≧ k(ε) ならば、|t(φ(n)) － p| < ε
この t(φ(n)) は、点 p の ε 近傍内に入っているので、（δ(r) として ε を考えると、）点 p における f の連続性から、
|f(t(φ(n))) － f(p)| < ε・・・①
一方、(★)から、t(φ(n)) = x(φ(n)) であり、
φ(n) という自然数について、
φ(n) < f(x(φ(n))) でした。
そのため、φ(n) < f(t(φ(n))) となります。
部分列の定義から、φ は自然数を定義域とする単調増加関数です。
k(ε) 以上の自然数 n に対して φ(n) は発散するため、f(t(φ(n))) の値も発散します。
これは、①に矛盾します。
（k(ε) 以上の自然数 n を増加させていくと、発散するので定点 f(p) との距離が開いていき、ε で抑え込めないため。）
よって、背理法から、f(I) は有界でなければならないことになります。【[1] の証明終了】
[2] の部分の証明
[2] f(I) における最大値と最小値の存在を示します。
値域 f(I) ⊂ R は[1]で有界であることを示したので、実数の連続性の公理から、上限と下限が存在します。
M = sup f(I)、m = inf f(I) とおきます。
ここで、自然数 n に対して、M － 1/n を考えると、M － 1/n は f(I) の上界ではないから、ある x ∈ I が存在して、M － 1/n < f(x)
このような x を1つとり、α(n) とすることで、数列 {α(n)} が定義できます。
M － 1/n < f(α(n)) ≦ M だから、
数列 {f(α(n))} は M に収束します。
ここで、{α(n) | n ∈ N} ⊂ I は有界だから、
収束する部分列 {α(φ(n)) | n ∈ N} が存在します。
この部分列についても、各自然数 n に対して、
M － 1/φ(n) < f(α(φ(n))) ≦ M
φ が単調増加のため、1/φ(n) が 0 に収束するため、数列 {f(α(φ(n))) も M に収束します。
一方、各自然数 n に対して、
a ≦ α(φ(n)) ≦ b だから、この部分列の収束値を w とすると、a ≦ w ≦ b なので、w ∈ I です。
よって、数列 {f(α(φ(n))) は f(w) ∈ f(I) に収束します。したがって、M は f(w) のことです。
また、自然数 n に対して、m + 1/n を考えると、m + 1/n は f(I) の下界ではないから、ある y ∈ I が存在して、m + 1/n < f(y)
このような y を 1 つとり、β(n) とすることで、数列 {β(n)} が定義できます。
m ≦ f(β(n)) < m + 1/n だから、数列 {f(β(n)) は m に収束します。
ここで、{β(n) | n ∈ N} ⊂ I は有界だから、
収束する部分列 {β(φ(n)) | n ∈ N} が存在します。
この部分列についても、各自然数 n に対して、
m ≦ f(β(φ(n))) < m + 1/φ(n) なので、φ が単調増加することから、数列 {f(β(φ(n)))} も m に収束します。
一方、各自然数 n に対して、
a ≦ β(φ(n)) ≦ b だから、この部分列の収束値を v とすると、a ≦ v ≦ b なので、v ∈ I です。
よって、数列 {f(β(φ(n)))} は f(v) ∈ f(I) に収束します。したがって、m は f(v) のことです。
以上より、値域 f(I) の上限 M と下限 m がどちらも f(I) に含まれるため、最大値が M で、最小値が m です。【[2] の証明終了】
さらに補足説明
[2]の証明で、部分列 {α(φ(n)) | n ∈ N} が実数 w ∈ I に収束するときに、点 w における f の連続性から M = f(w) を示しました。
この部分を近傍のイメージで考えて頂けるように証明を考えたつもりですが、不等式と論理を使って、この部分をより細かく証明します。
より、一般的な状況で証明します。
数列 {t(n)} が実数 s に収束し、関数 f が点 s において連続するときに、数列{f(t(n)) | n ∈ N} は f(s) に収束する。
ただし、任意の自然数 n に対して、t(n) は関数 f の定義域に含まれているとする。
この t(n) が先ほどの証明では、
α(φ(n)) や β(φ(n)) でした。
s が、w やv に当たります。
＜証明＞
ε を任意の正の実数とします。
f は s において連続だから、ある正の実数 δ(ε) が存在して、|x － s| < δ(ε) ならば、
|f(x) － f(s)| < ε … (ア)
数列 {t(n)} は s に収束するから、この δ(ε) に対して、ある自然数k(δ(ε)) が存在して、
n ≧ k(δ(ε)) ならば、|t(n) － s| < δ(ε)
今、|t(n) － s| < δ(ε) だから、(ア)より、
|f(t(n)) － f(s)| < ε
以上より、与えられた正の実数 ε に対して、k(δ(ε)) 以上の自然数 n について、
|f(t(n)) － f(s)| < ε となることから、数列 {f(t(n)) | n ∈ N} は実数 f(s) に収束します。【証明終了】
この内容を使って、先ほどの証明で、「数列 {f(α(φ(n)))} は f(w) ∈ f(I) に収束する」ということや「数列{f(β(φ(n)))} は f(v) ∈ f(I) に収束する」ことを書きました。
そして、数列に関する定理を使っています。
【補足の定理】
数列 {t(n)} が実数 p に収束し、かつ数列 {t(n)} が実数 q に収束するならば、p = q である。
この定理は、数列の収束先は、ただ 1 つということを示しています。
先ほどの証明では、「M に収束して、かつ w に収束した」ので、M と w が一致ということです。
もちろん、「m に収束して、かつ v に収束」ということについても、同じく m と v が一致ということです。
【補足の定理の証明】
正の実数を r とします。
r/2 > 0 より、数列 {t(n)} が実数 p に収束することから、ある自然数k(r) が存在して、
n ≧ k(r) ならば、|t(n) － p| < r/2
また、r/2 に対して、実数 q にも収束することから、ある自然数l(r)が存在して、
n ≧ l(r) ならば、|t(n) － q| < r/2
ここで、{k(r), l(r)} の最大値を i とおくと、
n ≧ i ならば、
|t(n) － p| < r/2 と、
|t(n) － q| < r/2 が同時に成立。
ここで、|p － t(n)| = |t(n) － p| であり、
三角不等式を利用すると、
|p － q| = |(p － t(n)) + (t(n) － q)|
≦ |p － t(n)| + |t(n) － q|
< r/2 + r/2 = r
以上より、
任意の正の実数 r に対し、|p － q| < r となることが示せました。
もし、p － q ≠ 0 と仮定すると、|p － q| > 0 です。
そのとき、|p － q|/2 > 0 なので、正の実数 r として |p － q|/2 を考えると、
|p － q| < |p － q|/2 です。
移項すると、|p － q|/2 < 0
両辺を2倍すると、|p － q| < 0
これは、|p － q| > 0であったことに矛盾します。
よって、背理法から、p － q = 0 となります。
つまり、p = q【証明終了】
これで、数列が収束するときに、収束する値が一定なことが証明できたので、すべての証明が補完されました。
ここまでで完了したのは、一次元ユークリッド空間内においての定理です。
先ほど示した定理は、大学数学で、一般の n 次元における有界閉集合上で定義された連続関数へと拡張されます。
連続関数 :有界閉集合上で定義された連続関数
連続関数が最大値と最小値をもつという定理を一般次元のユークリッド空間内の定理へと拡張をするにあたって、二つ補題を用意します。
【補題1】
空集合でない実数の集合Aに対して、sup A = M とする。
このとき、Mに収束する数列{a(n)}で、各自然数 n に対して a(n) ∈ A を満たすものが存在する。
＜補題１の証明＞
各自然数 n に対して、関数 b(n) を
b(n) = M – 1/n と定めます。
b(n) < M より、
b(n) は A の上限ではないから、ある要素 a(n) ∈ A が存在して、b(n) < a(n)
各自然数 n に対して、
M – 1/n < a(n) ≦ M
よって、はさみうちの原理から、
n → ∞ とすると、a(n) → M【証明完了】
この証明で、各自然数 n に対して A に含まれている a(n) を構成しました。
A ⊂ R なので、n∈A に対して a(n)∈R を対応させる関数を自分で定義したことになります。
各自然数に対して、b(n) をまず対応させ、さらに b(n) から a(n) を対応させることで、n と a(n) を対応させています。
上界であることの否定から a(n)∈A となります。また、数列 {b(n)} の方も、M に収束するので、はさみうちの原理を使って数列 {a(n)} が M に収束することを示しています。
もう一つの補題です。
【補題2】
空集合でない実数の集合 A に対して、inf A = m とする。
このとき、m に収束する数列 {a(n)} で、各自然数 n に対して a(n) ∈ A を満たすものが存在する。
【補題2】の証明
各自然数 n に対して、関数 b(n) を
b(n) = m + 1/n と定めます。
b(n) > m より、b(n) は A の下限ではないということから、ある要素 a(n) ∈ A が存在し、a(n) < b(n) です。
各自然数 n に対して、
m ≦ a(n) < m + 1/n
よって、はさみうちの原理から、
n → ∞ としたとき、a(n) → m【証明完了】
【補題2】は、【補題1】の inf 版です。
以下で拡張された定理の証明する際、[2] と書いている部分で、最大値の存在を示すときに【補題1】を使います。
最小値の存在を示すときには【補題2】を使います。
拡張された定理の証明
【拡張された定理】
R(m) の有界閉集合 D を定義域とする連続関数 f に対して、値域 f(D) は最大値および最小値をもつ。
＜証明＞
[1] f(D) が有界集合であることをまず示します。
f(D) が有界な集合でないと仮定します。
f(D) は上に有界でないから、「任意の自然数 n に対して、D 内の点 x が存在して、f(x) > n」(★)を満たします。
このような D 内の点 x(n) を任意に 1 つ選び、自然数 n に対応させます。
こうして、自然数全体から成る集合 N から D への関数 a を定義します。
（a:N → D を n∈N に対して a(n) = x(n) としています。）
集合 {a(n) | n∈N} は有界集合 D の部分集合なので、有界です。
※ {a(n) | n∈N} は R(m) の有界点列です。
よって、R(m) の有界点列は収束する部分点列をもつので、{a(n) | n∈N} の収束する部分点列を次のように表せます。
※ この収束部分点列の存在証明は、ノルム(norm) というブログに書いています。
収束する部分点列 A = {aφ(k) | k ∈ N} について、k → ∞ としたときの収束値を a とします。
【場合 1】 a が A に含まれていないとき
このとき、a は集積点となっています。
仮定より D は閉集合だから、a ∈ D です。
【場合 2】a ∈ A のとき
a ∈ A ⊂ D であり、関数 f は点 a ∈ D で連続だから、k → ∞ としたとき、
f(aφ(k)) → f(a) となります。
※ 閉集合（m = 1 のときは閉区間）を仮定されているのが、ここで効ききます。
点列の収束値が部分点列の値域である集合 A 内に含まれていなかったとしても、集積点は定義域 D 内に含まれています。
十分に接近している D 内の 2 点について、f が D において連続だから f による値 f(a) について、この図の最後の1行に書いている極限値が導かれます。
それでは、証明の続きです。
一方、（★）より、
各自然数 k について、f(aφ(k)) > n(k)
※ k > l のとき、n(k) > n(l) です。
よって、k → ∞ とすると、
f(aφ(k)) → ∞ です。
これは、k → ∞ としたときに、
f(aφ(k)) → f(a) であったことに矛盾です。
よって、背理法から、値域 f(D) は有界となります。【[1]の証明終了】
[2] 最大値および最小値の存在
[1] より、f(D) は有界だから、実数の連続性の公理により、f(D) は上限をもちます。
その上限を M = sup f(D) とおきます。
【補題1】より、各自然数 n に応じて、D の要素 y(n) が存在して、f(y(n)) = b(n) を満たします。
そのため、B = {y(n) | n∈N} という点列、つまり D の部分集合が定義できます。
D が有界なので、その部分集合である点列 B も有界です。よって、収束する部分点列が存在するので、それを次のように表せます。
収束する部分点列 B = {yφ(k) | k ∈ N} について、yφ(k) の収束値を b と置きます。
すると、D が閉集合なので、先ほどと同様に、
b が B に含まれていようが、含まれていまいが、b ∈ D です。
そのため、関数 f が点 a で連続なことから、f(yφ(k)) の収束値は f(b) となります。
ゆえに、M = f(b) です。
よって、この M が D における f の最大値です。
また、F(D) は有界だから、下限をもつので、
m = inf f(D) とおき、同様の議論をすると、m が最小値となります。【[2]の証明終了】
今回、証明した有界閉集合上で定義された実数値連続関数が最大値および最小値をもつという定理を 2 次元のユークリッド空間で用いることで、代数学の基本定理を導くことができます。
複素数を係数とする多項式が必ず解をもつということを保証する定理なので、とても基本となる定理の一つとなります。
※ 複素数体が、代数的閉体であるという内容です。
それでは、今回のブログを終了します。
読んで頂き、ありがとうございました。