常用対数 – 桁数 :小数首位の数などを計算の規則に基づいて考える【数II】

" 常用対数 – 桁数 “に関し、底が 10 の対数を使って、整数の桁数を求めるという内容について解説しています。
高校数学IIで学習する対数についての計算の規則に基づいて考えます。
また、不等式を絡ませて論理も使うので、高校一年で学習する内容とも関連して内容が複雑になります。
桁数の求め方を暗記するというより、自分で考えながら正確な計算と論理で結論を導くという意識で取り組むと総合的な数学の力が身につく良い内容かと思います。
それでは、具体的な数字を使いながら底 10 の対数についての計算を考察します。
常用対数 – 桁数
桁数を求めるときに使う不等式について説明します。
257 という整数を使って、具体的に説明します。
これは、3桁の整数(自然数)となっています。
3桁の整数というと、100 が最小になります。
そして、999 が 3桁の整数の中で最大となります。
そのため、
100 < 257 < 1000 となります。
ここで、指数を使って 10 の累乗という形で不等式を表してみます。
102 < 257 < 103 となります。
左側に等号が入っても良いので、
102 ≦ 257 < 103 という形で表すことを目指すのが、桁数を求める不等式です。
左辺の 10 の指数と、右辺の 10 の指数が 1 つだけズレているという状態を作ります。
すると、257 の桁数は、左側の 102 の桁数と一致します。
ここで、注意点です。
桁数と10の指数
101 の桁数は 2 桁です。
102 は 3 桁、103 は 4 桁です。
具体的に、これくらい記述すると、規則性が直観的に分かります。
一般に非負整数 n に対して、
10n の桁数は (n+1) 桁です。
万が一、忘れたら上のように10 の 1 乗から順に、いくつか具体的に書き出してみると、この規則が分かります。
※ 厳密に証明しようとすると、数学的帰納法という数学Bで学習する内容を使いますが、直観的に分かる通りで、この内容は事実として証明に記述できます。
今度は、10 の指数がマイナスの整数となっているときに、はじめて零でない整数が現れるのが小数第何位かということを押さえておきます。
10-1 = 0.1 なので、はじめて零でない整数が現れるのが小数第 1 位です。
10-2 = 0.01 →第 2 位、
10-3 = 0.001 →第 3 位 となります。
これについても、具体的に書き出すことで、すぐに規則性が分かります。
一般に、非負整数 n に対し、
10-n は小数第 n 位に、はじめて零でない整数が現れます。
ここまでの内容を踏まえて、具体的な典型問題で桁数を求める練習をしてみます。
常用対数 :ただし書きの小数を利用して
【練習問題】
820 が何桁の整数となっているのかを求めてください。
ただし、
log102 = 0.3010 として、必要に応じて使っても良いとします。
指数法則と対数についての公式を使います。
8 = 23 なので、
820 = (23)20 = 260 です。
よって、底 10 の対数を考えると、
log10820 = log10260
= 60 × log102 …①
ここで、「ただし書き」の近似された小数を使います。
60 × log102
= 60 × 0.4771
= 28.626 …②
②を①の右辺に代入すると、
log10820 = 28.626 です。
ここで、真数と底の関係から、
820 = 1028.626 となります。
y = 10x という指数関数は、底が 1 より大きいため、単調増加関数です。
そのため、
1028 < 1028.626 < 1029 です。
1028.626 は 820 だったので、
1028 < 820 < 1029 です。
これで、820 が (28+1) 桁、つまり 29 桁の整数ということが分かりました。
29 桁が答えとなります。
logaxt = t × logax という対数についての公式も使いました。
今度は、初めて零でない整数が小数第何位に現れるのかという問題を考えてみます。
初めて零でない整数が現れるのは?
【練習問題2】
0.520 は、小数第何位に初めて零でない整数が現れるのかを求めてください。
ただし、
log102 = 0.3010,
log103 = 0.4771 として、必要に応じて使っても良いとします。
ただし書きの内容を利用できるように、与えられた式を書き換えることから始めます。
0.5 = 1 ÷ 2 です。
そのため、
log100.520
= log10(1 ÷ 2)20
= 20 × log10(1 ÷ 2)
= 20 × (log101 - log102)
= 20 × (0 - log102)
= -20 × 0.3010
= -6.02 となります。
ここで、真数と底の関係から、
0.520 = 10-6.02 となります。
さらに、底 10 > 1 の指数関数が単調増加関数ということを使います。
すると、
10-7 < 10-6.02 < 10-6 となります。
すなわち、
10-7 < 0.5-20 < 10-6 です。
これで、小数第 7 位に初めて零でない整数が現れることになります。
これで答えが求まりました。
ところで、この小数第 7 位に現れる整数が、どんな整数かということが気になるところです。
そこで、さらに深く考察を進めます。
常用対数 :小数首位の数
0.03875 という小数を見てみます。
小数第 2 位に初めて零でない整数が現れています。
このように初めて現れる零でない整数を小数首位の数ということにします。
0.03875 の小数首位の数は 3 というように、この言葉を使うことにします。
先ほど、
log100.520 = -6.02 でした。
log103 = 0.4771 も利用して、
0.520 の小数首位の数を求めます。
-6.02 - 0.98 = -7 より、
-6.02 = -7 + 0.98 です。
log100.520 = -6.02 より、
0.520 = 10-6.02
= 10-7+0.98
= 10-7 × 100.98 です。
このため、
0.520 の小数首位の数は、
100.98 の先頭の数と一致します。
今度も底 10 の指数関数が単調増加関数であることを使います。
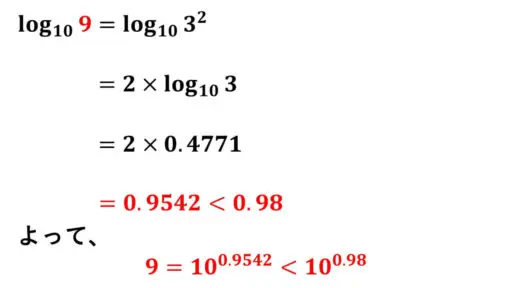
また、
100.98 < 101 = 10 です。
よって、
9 < 100.98 < 10 ということになります。
したがって、
100.98 を小数で表そうとしたときに、先頭に置かれる数が 9 と分かりました。
答えはすぐそこです。
0.520 = 10-7 × 100.98 より、
0.520 は、小数第 7 位に初めて零でない数 9 が現れるということになります。
すなわち、
0.520 の小数首位の数は 9 です。
このように、常用対数についての深い考察をする問題では、不等式の大小関係についての考察を正確に行うことが必要になります。
単調増加な関数のイメージと実数の大小関係についての高校一年以来の論理的な推論が大切になります。
関連する記事
今回の記事では使いませんでしたが、対数について、底を書き換えた方が良いときもあります。
底の変換公式という記事で、底の書き換えについて解説をしています。
また、指数の計算については、
指数方程式という記事で基礎的な内容を解説しています。
この内容は数学IIの範囲ですが、数学IIIでも使うときがあるので、早い段階で押さえておくと良いかと思います。
数学IIIについての記事も投稿しています。
常用対数では、底が 10 でしたが、数IIIでは自然対数も学習します。
ネイピア数という特別な底についての記事も解説しています。
数IIIでは、対数関数の微分も扱われるので、基礎的な公式を導出しています。
小数について高校の情報の授業で扱われる5進数の小数という記事も投稿しています。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。