必要条件 十分条件 | 数学で条件を満たす範囲を設定しておくことは基本となります!
" 必要条件 , 十分条件 " について、記事の前半で高校の数学の内容で基礎的なことを解説しています。
後半では、高校の数学から大学の数学へつなぐ内容について述べています。
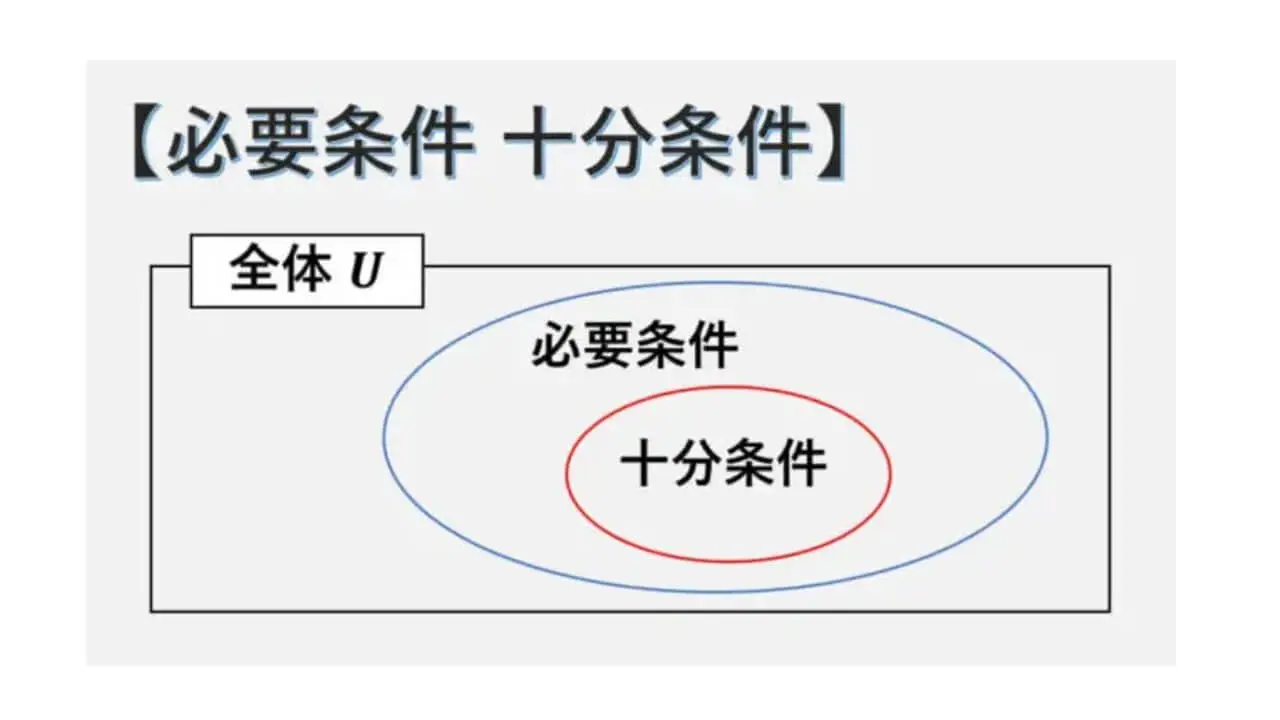
「条件 p を満たすならば条件 q を満たす」という命題が真であるとき、条件 p を十分条件、条件 q を必要条件といいます。
ここで、注意点は条件を満たすかどうかを、どういった範囲内の要素について判断するのかということを、はじめに設定しておくことが基本となります。
高校の数学IAの範囲の中だと、実数全体という範囲内で考えると、暗黙の了解で議論を進めることができるときもあるかと思いますが、数学IIBや数学IIICの範囲まで考えると、虚数が出てきたりと、扱う数学の対象が広くなります。
大学の数学も考えると、行列なども出てきて、より複雑になります。
もちろん数学IAの内容に限定しても、条件を満たすかどうかを判断する範囲を確定させないと、議論の内容に影響が出ることがあります。
この記事では、特に全体とする範囲を明確にして、必要条件と十分条件について解説をします。
条件を満たすかどうかを、どういった範囲内で考えているのかということを意識すると、数学への理解が深まるかと思います。
必要条件 十分条件 :逆についても考察する
【例1】
x を実数とする。
このとき、x = 2 は、
x2-x-2 = 0 という x についての二次方程式の解である。
この命題が真だと、「x = 2」ならば、「x についての二次方程式 x2-x-2 = 0 の解」ということなので、「x = 2」は十分条件ということになります。
まず、命題が真かどうかを確認します。
x についての方程式の解となっているのかどうかを確認するので、実際に代入をして計算をすると判断ができます。
22-2-2 = 0 なので、
x = 2 は、この二次方程式の解となっています。
そのため、命題が真なので、
「x = 2」は十分条件となっています。
条件 p ならば 条件 q という命題が偽のとき(反例が少なくとも一つ存在するとき)は、条件 p を十分条件とせず、条件 q を必要条件としません。
命題の真偽を確定させてから、十分条件や必要条件かどうかを決定することになります。
ここで、命題の逆も考えます。
逆が成立すると、「x = 2」が必要条件にもなります。
十分条件であり、なおかつ必要条件であるとき、必要十分条件といいます。
逆についても考察をした上で、最終的な決定をします。
そのため、一つの命題について、次の4つの可能性が考えられます。
・十分条件だが必要条件でない
・十分条件でないが必要条件である
・必要十分条件である
・十分条件でも必要十分条件でもない
先ほどの【例1】という命題について、「x = 2」という条件について、次の二つの可能性があります。
「十分条件だが、必要条件でない」と「必要十分条件である」という二つの可能性です。
十分条件であることは確かめたので、逆も成立して必要十分条件となるのかどうかを見極めることになります。
また、この命題(例1)では、x として考える範囲が実数全体となっています。
実は、この範囲を変えると、影響が出ることもあるので、議論の対象となる範囲を押さえておくことは大切になります。
必要十分条件かどうか
x を実数とする。
このとき、x2-x-2 = 0 という x についての二次方程式の解は x = 2 である。
「x2-x-2 = 0 という x についての二次方程式の解」というのが仮定条件です。
仮定条件を満たすのだけれども、結論条件を満たさないものを反例といいます。
実は、反例が存在することが、直接計算から分かります。
x = -1 が反例となることを確認します。
(-1)2-(-1)-2
= 1+1-2 = 0 です。
そのため、x = -1 は、「x2-x-2 = 0 という x についての二次方程式の解」という条件を満たしています。
しかし、「x = 2」という結論条件は満たしていません。
そのため、x = -1 は、この命題の反例ということになります。
反例が存在したので、この命題は偽です。
「x2-x-2 = 0 という x についての二次方程式の解」ならば「 x = 2」が偽ということです。
偽のときは、「x = 2」は必要条件でないということになります。
先ほどの議論と合わせると、「x = 2」は、「x2-x-2 = 0 という x についての二次方程式の解」であることの十分条件であるが、必要条件ではないということになります。
今度は、x は実数という範囲を異なる範囲にして、仮定条件と結論条件を同じままで命題を議論してみます。
どういう範囲内で議論をするのかという範囲を変えると、影響が出るということの具体例となります。
扱う範囲を変えてみる
【例2】
x を自然数とする。
このとき、x = 2 は、
x2-x-2 = 0 という x についての二次方程式の解である。
範囲を変更しました。
先ほどと同様に、命題は真で、
「x = 2」は十分条件となっています。
逆についての内容では影響が出ます。
x を自然数とする。
このとき、x2-x-2 = 0 という x についての二次方程式の解は x = 2 である。
x2-x-2 = (x+1)(x-2) です。
そのため、実数の範囲内で考えていると、
x2-x-2 = 0 という x についての二次方程式は、x = -1 と x = 2 という異なる二つの実数解をもちます。
今、x は自然数という状況の下で議論をしているため、x+1 ≠ 0 です。
そのため、x = 2 という可能性しかありません。
したがって、この命題は真となります。
そのため、「x = 2」が必要条件ということになります。
十分条件でもあったので、
「x = 2」は必要十分条件ということになります。
このように、議論をする範囲を変えると、影響が出ることもあるので注意です。
この例では、二次方程式の解がどちらも整数解となっていて、自然数の範囲に限定したから x が 2 しかあり得ないということになりました。
同じように x の範囲に着眼して、無理数の解と整数の解をもつときに、整数解だけに限定をするというような受験問題が出題されたりもします。
どの範囲で考えているのかということを、高校一年の段階から意識をしておくと良いかと思います。
二次方程式の解の存在範囲では、実数の範囲で議論をしていました。
ここまで、数学IAの範囲で述べましたが、数学IIBや数学IIICまで扱う対象が広がると、方程式の解の範囲を複素数の中で考えるときもあります。
例えば、x を複素数とすると、
x3 = 1 という x についての方程式の解で、1 とは異なる複素数解が出てきたりします。
※ 1の3乗根についての解説は、リンク先の記事で解説をしています。
ここからは、論理と合わせて数IIの軌跡の内容を述べておきます。
必要条件 十分条件 :軌跡と平行移動
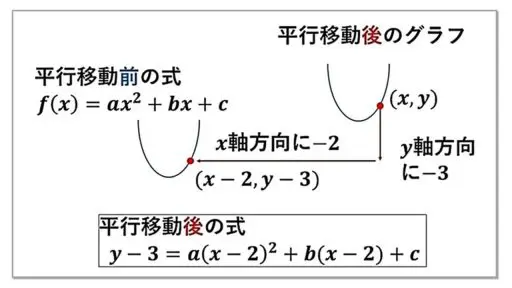
図の左上のところに、二次関数を表す定義式 f(x) を書いています。
y = f(x) = ax2 + bx + c . . . ★
平行移動をする前の二次関数のグラフを表す式が、y = f(x) です。
(p, q) が二次関数のグラフ上の点のとき、x に p を、y に q を代入したときに、左辺と右辺で等号が成立します。
また、(r, s)がグラフ上の点でないときは、x に r を、y に s を代入したときに、左辺と右辺で等号が不成立になります。
この二次関数のグラフを x 軸方向(横軸方向)へ 2、y 軸方向(縦軸方向)へ 3 だけ平行移動した後のグラフの式を求めます。
既に図の下に平行移動後のグラフを表す式を書いていますが、どうしてこのようになったのかを説明します。
関数のグラフを表す式というのは、そのグラフ上のどの点 (x, y) についても、x 座標の値と y 座標の値を代入すると左辺と右辺が等しくなる式のことです。
この平行移動後のグラフを表す式がどうして図の下に書いているようになるのかの説明は、実は単純な逆算ですが、軌跡の様子を具体的に見る良い例かと思います。
具体例で考える
数学IIで学習する軌跡ですが、グラフ上のどの点についても、x 座標の値と y 座標の値について成立する等式を求めることが本質となります。
そこで、平行移動後の二次関数のグラフ上の点を (p, q) とします。
平行移動前の二次関数のグラフ上のある点を x 軸方向へ 2、y軸方向へ 3 だけ移動してできたグラフ上の点が (p, q) となっています。
その「ある点」は、逆算すると、点 (p, q) を x 軸方向へ -2、y 軸方向へ -3 だけ平行移動した点ということになります。
点 (x, y) を x 軸方向へ -2、y 軸方向へ -3 だけ平行移動した点は (p - 2, q - 3) です。
この点 (p - 2, q - 3) は、y = f(x)のグラフ上の点なので、x に p - 2、y に q - 3 を★に代入すると、左辺と右辺で等号が成立します。
この等号が成立した式が図の下に書いている平行移動後の式です。
よって、平行移動後の二次関数のグラフ上の点 (x, y) について、代入すると等号が成立する式ができたということになります。
後、考えておかないといけないこととして、この等式を満たす実数の組が、必ず平行移動後の二次関数のグラフ上となるのかということです。
それを確かめてみます。
逆に、平行移動後の式を満たす任意の実数の組を (p, q) とすると、
実数 (p - 2, q - 3) は、平行移動前の二次関数のグラフを表す式の解となります。
よって、(p - 2, q - 3) は平行移動前のグラフ上の点ということです。
点 (p - 2, q - 3) を x 軸方向へ 2、y軸方向へ 3 だけ平行移動をすると平行移動後の二次関数のグラフ上の点です。
そのため、点 (p, q) は平行移動後の二次関数のグラフ上の点です。
必要十分条件の形にまとめる
y = f(x) を定義域を実数とする二次関数とする。
点(p, q) が、y = f(x) を x 軸方向へ 2、y 軸方向へ 3 だけ平行移動した後のグラフ上の点であることの必要十分条件は、(x, y) = (p, q) が方程式 y - 3 = f(x - 2) の解であることである。
<参考>
ちなみに、関数y = f(x)のグラフとは、
{(x, f(x)) | xは実数} という集合のことです。
<注意>
上で書いた理由の内容は、関数の定義式を全く具体的に計算していません。
この証明手順は、3次関数でも、対数関数でも三角関数でも使えます。
一般化すると、定義域を実数全体とし、各実数に実数値を対応させる関数について成立する平行移動に関する正しい内容になります。
数IIと数III で出てくる軌跡の理解は、二次関数の平行移動を通じて、分かりやすい具体例からスタートすると、スムーズに学習ができるかと思います。
最後に、大学の線形代数学で、方程式の解として行列を考えることがあるので、触れておきます。
多項式に行列を代入することをします。この多項式に行列を「代入する」ということも定義を押さえておかないと、議論できなくなってしまうので、注意です。
必要条件 十分条件 :大学の数学を少し
大学の数学についての記事も投稿しているので、少し大学の数学で使われそうな記号を使います。
実数全体から成る集合を R とし、
M(2, R) を R の要素を成分とする 2行2列の行列全体とします。
そして、M(2, R) における乗法単位元を E と表すことにします。
【多項式への行列の代入】
R-係数の多項式を
f(x) = anxn+…+a1x+a0 とする。
このとき、A∈M(2, R) に対して、
f(A) = anAn+…+a1A1+a0E と定義する。
もう少し正確に定義を述べると、
各項の aiAi (1 ≦ i ≦ n) は、
Ai という A を i 個で行列の乗法を計算した値です。
その Ai を ai∈R でスカラー倍したものが、
aiAi です。
そして、a0E は、単位行列を a0 でスカラー倍してできた行列です。
このようにして現れた (n+1) 個の 2行2列の行列の項すべてで、行列の加法を計算した値を f(A) と定義するということです。
このように、実数係数の多項式に、
M(2, R) という結合代数の要素を代入するということを定義しておかないと、議論ができなくなってしまいます。
anAn+…+a1A1+a0 としてしまうと、2行2列の行列と実数の加法という定義されていないものになってしまいます。
比較的に扱いやすい方程式で、解を考えてみます。
必要条件 十分条件 :解が行列
【例3】
x を実数を成分とする 2行2列の行列とする。
このとき、x = -2E は、
3x+6 = 0 の解である。
やはり【命題】なので、真偽の議論からスタートです。
f(x) = 3x+6 と置きます。実数を係数とする多項式です。
右辺についても、
g(x) = 0 と置きます。
代入したときに、定数項の部分に単位行列 E が現れるので注意です。
f(-2E) = 3(-2E)+6E
= 0E = O
よって、x = -2E は方程式の解です。
逆に、x = B∈M(2, R) を方程式の解とすると、
3B+6E = 0E = O より、
行列の計算から、
B = 3-1(-6E) = -2E となります。
はじめに、x = -2E が十分条件であることを確認し、後半で必要条件であることを確認しました。
3x+6 = 0 の行列解が、ただ一つであるという一意性の証明に当たります。
この一意であることを示すときに、行列の加法と実数体からのスカラー倍の定義を用いて計算を進めました。
先ほどの【例2】では、
整数環が整域ということを用いて、
(x+1)(x-2) = 0 だから、
x+1 ≠ 0 だから、
x-2 = 0 と結論づけました。
計算を進めるときに、推論の根拠を押さえる練習もしておくと良いかと思います。
この記事では、高校の数学以降の内容を見据えて議論をしてきました。
実は、中学の数学の段階から、必要条件と十分条件についての前段階のレベルで議論が扱われています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。