通過算 | 列車の長さを考慮して速さを計算した頃の定義を確認
" 通過算 “の具体的な内容を使って、定義に基づいて議論を進めるということの重要さについて解説をしています。
算数で学習した「速さ」についての公式を、そのまま使うだけだと答えと数字が一致しなかったという経験をもつ方も多いかと思われます。
単に速さの公式に数字を当てはめるだけではない通過算では、長さのある物体の移動距離の定義が関係しています。
それでは、定義を正しく認識するというトレーニングとして、通過算を例にして解説します。
通過算 :列車の長さで違いを知る
【速さの公式】
移動距離÷移動時間=速度
算数で学習する速さの公式です。
たとえば、次のような速さの問題を算数で学習します。
<例>
100mを50秒で移動したときの 1 秒あたりの速度を計算します。
100 ÷ 50 = 2 より、
1 秒ごとに 2m 進むと考えます。
そのため、毎秒 2 m という速度です。
※ 高校の物理では、これを平均の速さといい、移動する向きも考慮して速度といいます。
学習をし始めた頃は、この速さの公式に数字を当てはめると答えが得られました。
ところが、長さを考慮した物体の移動距離を考える問題も出てきます。
【問題】
毎秒4mで走る長さ20mの列車が、80mのトンネルを渡り始めてから渡り終わるまでに、かかる時間を求めてください。
答えを見ると、
(60+20)÷4 = 25
だから、25 秒かかると書いています。
ここで、違いに戸惑うことになります。
なにゆえに、20mという列車の長さを足したのかということです。
算数や数学では、式が意味を物語るということで、説明が省略されることが多いです。
そこで、内容を理解するときに、定義を押さえることから思考をスタートさせます。
早とちりに注意です
問題文に移動する物体の長さが書いてあるときは、その長さを足しおくと、安易に考えてしまうと、複雑な中学受験の問題や高校の物理などのレベルになると通用しなくなります。
この通過算という問題は、長さのある物体の移動距離の定義だけでなく、他の定義も関連してきます。
移動距離を、どのように考えれば良いのか。
徹底的に説明をします。
まずは、長さのある物体の移動距離から解説します。
通過算 :移動距離を徹底的に考える
【例題】
長さ 20mの列車が、
100mの橋を渡り始めてから渡り終わるまでに、10 秒かかったとします。
このとき、この列車の秒速を求めてください。
ここで、長さのある物体の移動距離を、どのように定義しているのかを押さえておくことが大切になります。
移動する物体の一か所に印を付けます。
この付けた印が動いた距離の長さを、物体の移動距離と定めます。
列車のどこに印をつけても良いのですが、それぞれの問題を考えるときに、扱いやすい所に印をつけるようにします。
ただし、速さを考えているので、時間をどのように測定するのかも決めておかなければなりません。
橋を渡り始めてから渡り終わるまでに 10 秒という例題ですが、時間の計測についても定義があります。
列車の先頭が、橋の端にさしかかった瞬間から、移動時間を計測し始めます。
文章だけだと、内容がつかみにくいので、図も用いて見える化しつつ説明を続けます。
移動時間も考える
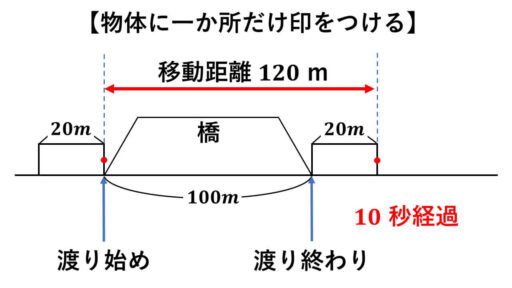
列車の先頭に印をつけて、移動距離を計測します。
列車の先頭が橋の(左)端にさしかかった瞬間から移動時間の計測がスタートします。
そして、時が刻まれます。
時間の計測を始めたら、いつ終えるのかということも決めておかなければなりません。
移動時間の計測の終了は、列車の最後尾が橋の(右)端を離れる瞬間です。
これで、移動時間の計測を終えます。
移動時間を計測し始めてから、計測を終えるまでに経過した時間が、列車の移動時間です。
この移動時間が、【例題】では 10 秒ということです。
移動時間の計測を止めたときまでに、付けた印が動いた距離が移動距離です。
図より、
100 + 20 = 120 (m) が列車の移動距離となります。
移動時間は 10 秒です。
このようにして、
(100 + 20)m と、列車の長さを足したわけです。
※ 移動する物体の長さを足すとは限らない問題もあるので、定義に基づいて移動距離を考えることが必要になります。
これで、移動距離と移動時間が確定したので、列車の速さを求めることができます。
120 ÷ 10 = 12 より、
毎秒 12m となります。
これで、答えに辿り着くことができました。
この通過算の内容は、中学の数学でも方程式の文章問題として出題されることがあります。
さらなる練習に、方程式の問題を解説します。
通過算 :方程式を考える
【練習問題】
毎秒 25 m の列車が橋を渡り始めてから渡り終わるまでに 10 秒かかったとします。
また、この毎秒 25m で走る列車が、踏切にさしかかってから、通過するまでに 2 秒かかったとします。
ただし、踏切は長さをもたない1点として扱うことにします。
このとき、列車の長さと橋の長さを計算してください。
中学の数学では、未知数を文字で置き、方程式を作り、方程式を解くことで未知数を決定します。
列車の長さを a(m)、橋の長さを b(m) として方程式を作ります。
等しい数量をイコールでつなぐことで、方程式(等式)を作ります。
まず、橋の内容から等式を導きます。
橋を渡り始めてから渡り終わるまでに 10 秒かかったことから、毎秒 25m なので、移動距離が計算できます。
25 × 10 = 250(m) が移動距離です。
移動距離は、先頭が橋の(左)橋にさしかかってから橋の(右)橋を離れる瞬間までの 10 秒で移動した距離でした。
そのため、
a+b = 250 …①
もう一つ方程式を作ります。
今度は、実用的な数学で、しばしば使われる考え方を使います。
点の長さ0
数学を使って、実用的な計算をするときに、理想的な状態で計算をするときがあります。
数学の物理への応用や化学への応用といったときに、点には、長さや面積や体積が無いとして 0 と見なすという考え方です。
そんな考え方を取り入れて練習問題としました。
長い線路という道のりの中で、たった一つの踏切の部分を走る長さは微小であるということで、踏切の所を通過するときの距離を 0 とするということです。
橋くらいの大きさだと、長さを考えて b(m) としています。
踏切については 0(m) です。
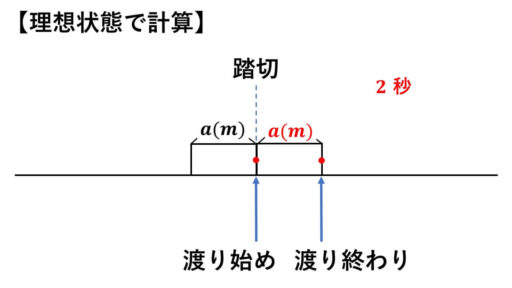
踏切の部分を 0m だと見なすと、列車が踏切にさしかかってから、通過するまでの 2 秒で先頭の印が動いた移動距離が、列車の長さ a(m) そのものになります。
そのため、毎秒 25m で 2 秒間に a(m) を走ったということです。
a = 25×2、
つまり、a = 50 …②
これで、a+b = 250 …① に ② を代入して、b の値も求めることができます。
50 + b = 250 より、
b = 200 です。
以上より、
列車の長さ 50m、
橋の長さ 200m と分かりました。
この練習問題では、踏切の部分が 0m という理想状態を想定して計算を進めました。
実は、この理想状態において計算をするということが、既に小学校の算数において使われています。
それが、この記事のはじめで述べた内容です。
通過算 :理想状態で再考
【長さ0の物体の移動】
車が 2 時間で 80km を走ったときの時速
算数で速さの計算を学習したときに、このような内容が出てきます。
80 ÷ 2 = 40 で、
時速 40km ということです。
この内容のように、移動する物体の長さを全く考えていない計算です。
先ほどは、移動する線路の一部の踏切の部分が、全体の距離の中で微小と考えて 0 m としました。
速さの学習をし始めるときに、簡単のために移動する物体の長さを 0 として、速さの公式を使う練習をしていると考えるとスムーズかと思います。
(0 + 80) ÷ 2 は、
80 ÷ 2 = 40 ということです。
実用的な計算を考えるときに、長さの無い 0 として、スムーズに計算をするという考え方です。
移動する物体の長さを考慮するのか、考慮しないのかは出題される問題によるので、文章問題を練習して、見分ける練習をしておくのも良いかと思います。
速さに関連する内容
この通過算という記事では、算数や中学一年・二年の内容を用いて述べてきました。
最後の方で、高校以降のことを考えて理想的な誤差の扱いについて触れました。
高校の数学IIになると、微分と速さが関連してきます。
中学の数学の内容については、一つ前の記事で食塩水についての方程式の問題を解説しています。
また、時間経過にともなって角度の大きさが変化する内容も中学の数学や理科で扱われます。
円を一周したときに、動いた角度は360°です。
1 日は 24 時間なので、1 時間あたりに、どれだけの角度を動くのかを計算できます。
星が動く速さが一定であるという前提の下、360°を24等分します。
360÷24 = 15 より、
1 時間あたりに 15°動くということになります。
これで、単位時間あたりに動く星の角度が設定できました。
理科と合わせて、回転運動の下地となる内容についての内容も述べておきます。
星の動きについて
星が 1 時間あたりに 15°動くということは、動く時間が 2 倍・3 倍になると動く角度も 2 倍・3 倍になるということです。
星が動く時間が 2 時間だと、
15 × 2 = 30 より、
30°動くというように計算できます。
この内容を、比で表しておくと、計算する道が明確になります。
1 : 15 = 2 : 30 です。
時間の方を 2 倍すると、星の動く角度の大きさも 2 倍されます。
1 : 15 = 3 : 45 でもあります。
星の動く角度の大きさを 15 から 45 へと 3 倍すると、時間の方も 3 倍されています。
まさに、片方を 2 倍・3 倍にすると、もう片方も 2 倍・3 倍になるという関係です。
比で扱うと、計算の過程が算数・数学の理論によって規定されているので、計算を円滑に進めることができます。
たとえば、星が 90°動くのにかかる時間はどれだけか計算してみます。
未知数を x と置いておき、比を使って式をつくります。
星が x 時間で 90°動いたとして、比を使って表します。
1 : 15 = x : 90 です。
注意点は、左側の値は動いた時間、右側の値は動いた角度で揃えておくことです。
すると、内項の積が外項の積と等しいという理論が使えます。
15 × x = 1 × 90 より、
15x = 90 です。
これで方程式ができました。
後は、計算のきまりに基づいて計算を進めると、解である未知数の値に辿り着きます。
両辺を 15 で割って、
x = 90÷15 = 6 となります。
これで、星が 90°動くのに 6 時間かかったということが分かりました。
ここまで、整数だけで計算を述べてきましたが、小数も使った内容を扱ってみます。
小数・分数が出てくると、イメージがつかみにくくなるので、掛け算をするのか割り算をするのかと混乱するかもしれません。
しかし、理科の内容を比で表しておくと、内項の積と外項の積が等しいということから方程式へと書き換えることができるため、道筋が明確になります。
時間計算を小数・分数で
【問題】
星が 12.6°動くのにかかる時間を計算する。
先ほどと同じように、x 時間かかるとします。
15°より小さい 12.6°ですから、かかった時間は 1 時間よりも短い時間だと分かりますが、正確に x の値を計算で求めます。
1 : 15 = x : 12.6 なので、
内項の積と外項の積が等しいことから方程式をつくります。
15 × x = 1×12.6
x = 12.6÷15
= 0.84 となります。
これで、12.6°動くのに 0.84 時間かかったということが分かりました。
割り算の計算ですが、逆数を用いて分数の掛け算にすると約分してスムーズに計算できるときもあります。
約分をした後、再び割り算に戻すと、より小さな数の割り算を計算するのと同じ計算結果となります。
12.6÷15
= 12.6 × 1/15
分子と分母を 3 で約分できます。
4.2 × 1/5 と同じ値です。
割り算に戻すと、
4.2 ÷ 5 です。
このため、
12.6÷15
= 4.2÷5 = 0.84 と暗算で計算できました。
分数を使って約分ができるとき、直接に筆算を使わなくても、より簡単な計算で同じ値を求められるときもあります。
そんなチャンスがあれば、分数の計算をしてみるのも良いかと思います。
また、割り算をしたときに、割り切れないということが起きるときがあります。
割り切れないときは、もうこれ以上は約分できない分数を最終的な答えとします。
※ これ以上は約分ができない分数のことを既約分数といいます。
練習問題
【問題】
オリオン座を見つけてから、
3/11 時間の間にオリオン座が動いた角度の大きさを計算してください。
分数が使われていても、今までと同じように比から方程式をつくります。
求める動いた角度の大きさを x とします。
1 : 15 = 3/11 : x という比の関係です。
内項の積と外項の積が等しいことから、次の方程式(等式)が得られます。
x = 15 × 3/11
分子どうしを掛ける分数の掛け算を計算します。
x = 45/11 となります。
45/11 度というのが、答えとなる角度の大きさになります。
分数が使われていたとしても、同じ流れで比を使って計算を進めることができます。
ちなみに、45/11 が、これ以上の約分ができないということを確認しておきます。
約分できるかどうかは、素因数分解ができると最終的な判断ができます。
※ 分子と分母の最大公約数が 1 と分かれば、これ以上は約分できないことになります。
45 = 32×5 が、分子の 45 の素因数分解です。
分母の 11 は素数なので、このままで分解された状態です。
45 の素因数である 3 や 5 と、分母の 11 の最大公約数が 1 です。
そのため、45/11 は、もうこれ以上は約分ができないと分かります。
このように算数や中学の数学の計算で触れる分数の約分ですが、高校の数学にも関連します。
【関連する記事】
今回の記事では、時間計算に関連して比を使いました。
黄金比という記事で、特殊な比の値について、中学で学習する図形を用いて解説をしています。
回転運動による角の大きさの変化については、
等速円運動という数3の微分の内容の記事も投稿しています。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。