真数と底 | 底を何乗すると真数となるのかを示す値が対数関数の取る値【逆対応について理解】
" 真数と底 “についての関係を理解することは大切になります。なぜなら、対数関数と指数関数のグラフが y=x について対称となっているということを、逆対応の考えから考察する際に、基本となるからです。
図形的な情報を裏打ちする数学の論理について、関数のグラフを集合を用いて解説しています。
なぜ y=x に関し対称なのか。この理由を理解することで、数学２の内容から、数学３，しいては大学の数学へとつながります。
まず、対数関数の定義から説明します。一般的な文字を使った定義から、具体的な数字を使って、定義の内容を確認します。
対数関数の定義を押さえてから、関数のグラフを集合を用いて解説をします。
指数関数が対数関数の逆関数であるということが、座標平面において、直線 y = x と対称となっていることと、どう関係しているのかを理解するための内容になります。
難しい大学受験の問題で、対応関係を基礎とした問題が出題されることもあります。
また、理系の方ですと、数学３で逆関数を学習するので、その基本として押さえておきたい内容となります。
では、定義から解説します。
真数と底 :定義の解説
【対数の定義】
a を 0 より大きく、1 ではない実数とする。また、b を 0 より大きい実数とする。
このとき、a の指数となる実数で、その指数乗が b となるものを logab と表す。
f(x) = ax という底を a とする指数関数のグラフの概形は分かっています。
0 < a < 1 だと、右下がりのグラフで、値域は、0 から +∞ の間です。
1 < a のときは、右上がりのグラフで、値域は、同じく 0 から +∞ の間です。
いずれにせよ、指数関数のグラフは単調関数となっています。
そのため、b > 0 が与えられると、ax = bを満たす実数 x が、ただ一つのみ決まります。
この指数 x の値が、logab です。
logab は、実数なので、
x = logab を y = ax に代入することができます。
logab の定義から、
alogab = b となります。
文字を使っているので、難しそうな雰囲気になっていますが、具体的な数字で、この対数の定義を確認します。
数字を使った例
f(x) = 2x という底 a が 2 である指数関数と、真数 b として 8 という 0 より大きい実数を考えます。
2x = 8 という等式を満たす実数 x が、
log28 の値です。
f(x) = 2x のグラフは、右上がりのグラフで、値が 3 となるときの指数 x は、ただ一つのみ定まります。
2 を 3 乗すると 8 になるので、
x = 3 のとき、23 = 8 となります。
よって、log28 = 3 となっています。
明確に値が分かっているときは、
log28 = 3 と表すことができます。
今度は、正の実数 x に対して、1 つの値を対応させる対数関数について説明をします。
真数と底 :対数関数の対応
a を 0 より大きく、1 ではない実数とします。また、x を正の実数とします。
今度は、x を真数として考えます。
与えられた状況で、底 a の指数で、その指数乗をした値が x となるように指数 c が定まります。
f(t) = at の値域が、0 から +∞ の間であり、グラフが単調です。
そのため、
ac = x を満たす t = c が、ただ一つ存在します。
よって、x に対して、c を対応させることができます。
これが、g(x) = logax という対数関数の定義です。
正の実数 x に対して、
ac = x を満たす実数 c を対応させるという関数です。
※ 一般に、手計算では、この c の値が具体的に、どんな数かは不明になることが多いです。しかし、そのような実数 c が、ただ一つのみ存在しているので、対数関数が定義できます。
また、具体的な数字を使って、対数関数の例を見てみます。
対数関数の例
g(x) = log2x という底が 2 の対数関数です。
x = 16 に対して、g(16) という値を対応させています。
この g(16) は、定義から具体的に決定できます。
2c = 16 を満たす実数 c が、g(16) の値です。
24 = 16 なので、c = 4 ということになります。
ゆえに、log216 = g(16) = 4
毎回、このように対数関数の値が明確に手計算で求まるわけではありませんが、整数を使ったシンプルな例を通して、真数と底の関係を押さえておくと良いかと思います。
次に指数関数の逆関数が、対数関数となっていることを解説します。定義の通りに対応を確認すると、逆対応になっていることが分かります。
逆対応の確認
a を 0 より大きく、1 ではない実数とし、
実数 x に対して、f(x) = ax とします。
また、正の実数 t に対して、
g(t) = logat とします。
※ 対数関数の定義域は、t > 0 となっています。
f(x) = ax > 0 なので、対数関数の定義域の範囲内の実数です。
そのため、f(x) = ax という実数に対して、対数関数で値を対応させることができます。
g(f(x)) = logaax です。
ここで、対数の定義から、
logaax という実数は、a の指数で、その指数乗をすると真数 ax となるものでした。
今、a を x 乗すると、ax となっているので、
logaax = x です。
よって、g(f(x)) = x
この内容を整理してみます。
指数関数によって、x に ax を対応させました。
対数関数によって、ax に x を対応させています。このため、対数関数の対応は、指数関数の対応の逆対応となっています。
今度は、先に対数関数で正の実数を移してから、その値を指数関数で移してみます。
t を正の実数とすると、g(t) = logat
この実数 g(t) を指数関数で移すと、
f(g(t)) = alogat です。
対数の定義から、
logat という実数は、a の指数で、その指数乗をすると真数 t となるものです。
よって、alogat = t
つまり、f(g(t)) = t
t に対して、対数関数で logat を対応させました。
そして、logat を指数関数で移すと t となりました。
やはり、指数関数と対数関数の対応は、それぞれ互いに逆対応となっています。
この逆対応をxy-座標平面におけるグラフで考えるときがあります。
y = x について指数関数のグラフと対数関数のグラフが対称となっている理由を、真数と底の関係から考察します。
そのために、座標平面上のグラフとは内かということを集合を用いて解説します。
真数と底 :y=xに関して対称とは
a を 0 より大きく、1 ではない実数とし、
y = f(x) = ax という底が a の指数関数を使って、座標平面上の関数のグラフを説明します。
先ほど説明した逆対応を座標平面において図形的に表現すると、イメージがつかみにくいので、ここは理解するのに注意した方が良さそうな内容です。
y = f(x) という（指数）関数が、
実数 x に対して f(x) という値を対応させていたとします。
このとき、点 (x, f(x)) を座標平面における関数のグラフ上の点として認識します。
x座標の値 x に対応する値を y座標に記した組が、その関数のグラフ上の点です。
y = f(x) のグラフ上の点を全て集めた集合は、
{(x, f(x)) | x は実数} です。
今回は指数関数なので、f(x) = ax となっています。
さらに、y = g(t) = logat のグラフ上の点全体の集合も考えると、
{(t, g(t)) | t > 0} です。
定義域と値域の対応を意識しながら、
x = s のときについて指数関数のグラフ上の点と対数関数のグラフ上の点を見比べます。
※ リンク先では、数学３の合成関数や逆関数について解説をしています。
点 A(s, as) が指数関数のグラフ上の点です。
対数関数の対応は逆対応なので、as という正の実数に対して、s を対応させていることになります。
よって、g(as) = s なので、
点 B(as, s) が対数関数のグラフ上の点です。
この点 A と点 B は、
直線 y = x に対称な位置にあることが、次のようにして分かります。
中点と傾きから考察
点 A(s, as) と点 B(as, s) の中点 M の座標を求めてみます。
x座標の値どおしの平均値が中点の x 座標の値です。そして、y座標の値どおしの平均値が中点の y 座標の値です。
(s + as) ÷ 2 = (as + s) ÷ 2
よって、中点 M の x 座標と y 座標の値は、どちらも同じ値となっています。
x 座標と y 座標の値が、どちらも同じ値となっている点は、
直線 y = x 上の点です。
したがって、点 A と点 B の中点 M は、
直線 y = x 上の点です。
さらに、直線 AB の傾きを求めてみます。このときに、分母が 0 にならないように場合分けをして考察します。
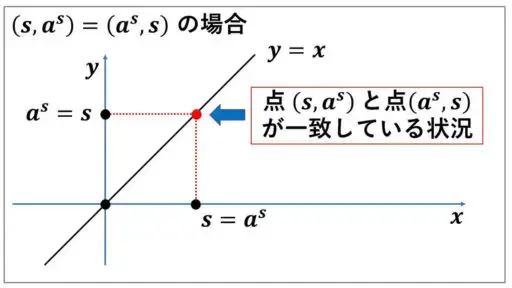
【s = as のとき】
このとき、指数関数のグラフ上の点について、
点 (s, as) = (s, s) は y = x 上にります。
この点と対になる対数関数のグラフ上の点は、
点 (as, s) = (s, s) です。
したがって、点 (s, as) と点 (as, s) は一致しています。
そして、x座標の値と、y座標の値が等しいことから、
直線 y = x 上の点です。
つまり、指数関数のグラフと対数関数のグラフの交点が、
(s, as) = (s, s) で、y = x 上に交点があるという状態です。
次に、s = as ではない場合を次に考察します。
【s ≠ as の場合】
このとき、二点 A(s, as) と B(as, s) を通る直線の傾きを計算します。
(s－as)÷(as－s) = －1
直線 y = x の傾きは 1 なので、
直線 AB との傾きの積が －1 です。
二直線が垂直に交わるのは、二直線の傾きの積が－1 となるときなので、直交していることが分かります。
点 A と B の中点 M は y = x 上にあったので、
直線 y = x が線分 AB の垂直二等分線となっています。
よって、点 A(s, as) と点 B(as, s) は、
直線 y = x について対称な位置にあるということが分かりました。
指数関数によって、s に as を対応させ、対数関数によって、as に s を対応させているという逆対応の関係が効いています。
特殊な場合が、先ほど述べた一致しているということです。
今回、数学２の対数関数の内容を述べました。大学の複素解析では複素数を定義域とする複素指数関数や複素対数関数が扱われます。
また、代数的な二項演算に関連して多項式の x の指数の部分を計算することも大切になります。
指数について、基本となる内容については、指数方程式という記事で解説をしています。
対数については、底の変換公式という記事を投稿しています。
常用対数という底 10 の対数を解説しています。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。