無限降下法 | 空ではない自然数全体の部分集合の最小値の存在を利用した証明論法【植木算を証明】
" 無限降下法 “と高校の数学で呼ばれる証明論法の使い方を、具体的な自然数に関する命題を用いて解説しています。
植木算でお馴染みの間の個数についての命題を証明します。
直観的に明らかな内容を用いることで、無限降下法の論理構成を集中して観察することができるかと思います。
はじめに、この論法を支える自然数の性質を述べ、それに基づいて実践的に証明を行います。
比較的に簡単な命題の証明で使用することで、論理の型の把握に焦点を当てます。
無限降下法 :自然数に関する命題
数学では、真偽を明確に判断できるものを命題といいます。
この命題ですが、自然数 n に応じて 1 つの命題が定まるときがあります。
そのときに、自然数 n に関する命題 P(n) と表すようにします。
算数で出てくる植木算の内容を命題の形で表してみます。
n = 2 のときの命題 P(2) として、次の命題を考えます。
【命題P(2)】
直線上に木を 2 本植える。
植えた木と木にできる間隔の個数を間の個数と呼ぶことにする。
このとき、間の個数は、(2－1) 個である。
「木 -間- 木」と、確かに間の個数は 1 となっているので、この命題は真です。
植えた木の本数が 2 本ということで、自然数 2 に応じた命題 P(2) です。
より一般的に、木を n 本植えたときの命題 P(n) を考えます。
【命題P(n)】
直線上に木を n 本植える。ただし、n は 2 以上の自然数とする。
植えた木と木にできる間隔の個数を間の個数と呼ぶことにする。
このとき、間の個数は、(n－1) 個である。
先ほど、n = 2 のときに、具体的に命題 P(2) が成立することを確認しました。
ここで、「2 以上のどんな自然数 n についても、命題 P(n) が真となっている」と証明することを考えます。
2 以上の自然数は無限個あるので、個々に調べていては永遠に終わりません。
「どんな自然数 n についても命題 P(n) が真」ということを証明するときに使うチャンスがある論法が無限降下法です。
数学的帰納法の変形版と思っておくと良いかと思います。
この論法の背景の内容は、大学の集合論の入門的な内容で扱われます。
そこで、取り挙げられる自然数全体についての特徴的な性質を利用した証明論法となります。
自然数全体Nの性質
自然数全体から成る集合を N と表すことにします。
この N について、次の性質があります。
【N の性質】
N の空集合でないどんな部分集合にも、その部分集合内の最小値が存在する。
この性質は、大学の数学の用語を使うと、自然数全体 N は整列集合ということを意味します。
※ この N についての性質の証明は、超限帰納法という大学数学についてのブログ記事で解説をしています。
抽象的な内容なので、具体例を挙げます。
S = {7, 11, 52} という N の部分集合は、空集合ではありません。
この S 内に含まれている自然数の中では、7 が最小値となっています。
このように、N から、空集合ではないどんな部分集合 S をとってきても、その S 内には、S における最小値が必ず存在するということです。
この N についての性質を利用した証明論法が無限降下法です。
2 以上のどんな自然数 n についても命題 P(n) には反例が存在しないということが分かると、2 以上のどんな自然数 n に対しても命題 P(n) が真ということになります。
そこで、背理法を使い、ある 2 以上の自然数 n が存在して、P(n) が偽となっていると仮定して矛盾を導きます。
その矛盾を導くときに、2 以上の自然数 k で、命題 P(k) が偽となる自然数を全て集めます。
そのような k たちから成る集合は自然数全体 N の空でない部分集合です。
すると、自然数の性質から、その部分集合には最小値が存在することになります。
この最小値を使って、矛盾を導くというのが無限降下法の論理的な骨格です。
では、無限降下法を用いて植木算の内容を証明します。
無限降下法 :植木算を証明する
【命題 P(n)】
直線上に木を n 本植える。ただし、n は 2 以上の自然数とする。
植えた木と木にできる間隔の個数を間の個数と呼ぶことにする。
このとき、間の個数は、(n－1) 個である。
＜証明＞
2 以上のある自然数 k が存在して、命題 P(k) が偽だと仮定します。
{k∈ N | k ≧2, P(k) が偽} を S と置くと、今、S は空集合ではない N の部分集合です。
自然数についての性質から、S において、最小値が存在します。
その S における最小値を t とします。
P(2) は、上で具体的に述べたように真です。
そのため、t は 3 以上の自然数ということになります。
そのため、t－1 ≧ 2 です。
1 番目に植えた木から (t－1) 番目に植えた木についての間の個数を求めます。
t－1 < t より、t の最小性から、
命題 P(t－1) は真ということになります。
ここで、(t－1) 本の植えた木に対して、真である命題 P(t－1) を適用すると、1 本目から (t－1) 本目までの木について、間の個数が (t－2) 個となります。
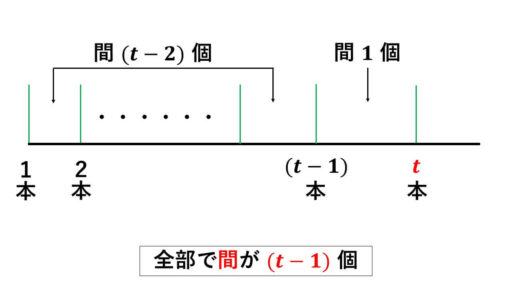
よって、さらに t 本目の木を植えると、間の個数が 1 増えるので、
1 本目から t 本目までの木について、間の個数が (t－1) 個となります。
これは、命題 P(t) が成立していることになり、P(t) が偽であることに矛盾します。
以上より背理法から、
2 以上のどんな自然数 n についても命題 P(n) が成立することになります。【証明完了】
この自然数の性質を利用した最小の反例から、矛盾を導くのが無限降下法です。
植木算と同じく算数で正しいということを習うのだけれども、厳密証明は大学で扱うというものに除法の原理（検算）があります。
この検算の証明にも、無限降下法は役立ちます。
関連する記事
以前に投稿した次の記事で、大学の数学用に検算を無限降下法で証明をしています。
検算が成立することによって、整数全体 Z がユークリッド整域となっています。
整数環はユークリッド整域ということは、環論の入門で学習する基本的な事実の一つとなります。
大学の数学を学習するときに、整列集合についての内容が絡むので、無限降下法の証明骨格を通じて整列集合というものを意識する場として、無限降下法で植木算の証明を押さえておくというのも手です。
しかし、算数の段階で、この証明は苦しいので、大学の初等整数論や環論の入門内容を学習するときに、厳密な証明をするという流れになっています。
この証明は、割る数を自然数としておき、その自然数についての命題として、ある自然数について偽となる命題があったと仮定して矛盾を導きます。
証明の骨格は、今回の証明と同じになっています。
では、植木算を証明したので、この内容を使って、数列についての内容を導いておきます。
無限降下法 :得られた命題の適用
数学では、証明しようとする命題の真偽に関係なく、既に証明されている正しい命題を適用することができます。
そこで、先ほど無限降下法を使って証明した植木算の内容を使って、等差数列の公式を導きます。
初項 a, 交差 d の等差数列 {an} の一般項を導きます。
第 1 項から第 n 項までの n 個の項と項の間の個数は、植木算より、(n－1) 個あります。
この間の一つずつに交差 d を加えます。
すると、第 1 項の値 a に、
交差 d を (n－1) 個だけ加えると、
第 n 項の値 an となります。
すなわち、
an = a+d×(n－1) です。
これで、一般項 an を、与えられた初項と交差を用いて表すことができました。
さすがに、ここまで植木算を厳密に証明することなく、高校の数学では植木算を自然と使って等差数列の一般項を求めています。
今回の記事では、無限降下法の証明の骨格を明確に記せる例として植木算を証明しただけなので、そこまで植木算の厳密証明を気にしなくて大丈夫です。
植木算の発想は高校の数学でも使えるチャンスがあれば、厳密な証明は気にせずに気軽に使えます。
同様の考察
初項 b, 公比 r の等比数列 {bn} についても、植木算を適用して一般項が得られます。
第 1 項の値 b に、
交比 r を (n－1) 個だけ掛けると、
第 n 項の値 bn となります。
そのため、
bn = b×rn-1 となります。
このブログでは、算数で学習した植木算から、高校や大学の数学につながる内容として述べました。
また、4の倍数という記事では、算数の内容や社会的な一般教養として日付の計算について解説をしています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。