調和数列 | 逆数をとると等差数列という定義

" 調和数列 “の定義は、それぞれの項を" 逆数 “とする項たちから成る数列が等差数列となっているということです。
定義に基づいて、具体例を用いて理解をしておくと、その後の学習に役立つ内容です。
数学3も見越して、合成関数の考え方に触れる良い機会ともなります。
高校一年の頃から、合成関数の考え方は、背後で使われているのですが、はっきりと意識をして認識できると数学の良い基礎となります。
もとの数列 {an} と、その各項の逆数を項とする数列の両方が調和数列の定義に使われます。
どちらの数列が、もとの数列としているのかを見切っておかないと混乱するので、毎回、意識すると良いかと思います。
それでは、調和数列について、例を用いながら基礎から解説します。
調和数列 :定義と具体例
【定義】
数列 {an} の各項の逆数を項とする数列を {1/an} とする。
数列 {1/an} が等差数列となっているとき、もとの数列 {an} を調和数列という。
定義に、二つの数列が使われているので、具体的な数列の問題を解くときに、どちらの数列を、もとの数列としているのかを意識することが大切になります。
調和数列となっているのかを定義に基づいて判断するのに、具体例があると分かりやすいかと思います。
次に具体例を挙げますので、どちらが、もとの数列なのかを押さえた上で、もう一方の数列が等差数列となっていることを確認します。
調和数列の例
次のような数列 {an} が与えられたとします。
つまり、1, 1/2, 1/3, …
自然数 n に対して、{an} の第 n 項の値は、
an = 1/n となっています。
この数列 {an} が、もとの数列です。{an} は等差数列となっていません。
実際、1/2 - 1 = -1/2 ですが、
1/3 - 1/2 = -1/6 なので、差が一定ではありません。
ところが、数列 {an} の各項の逆数を並べてできる次の数列 {1/an} は等差数列となっています。
1, 2/1, 3/1, … と、逆数をとって並べたものが等差数列となっています。
自然数 n に対して、{1/an} の第 n 項の値は、
an = n となっています。
分母が全て 1 なので、初項 1, 交差 1 の等差数列です。
したがって、数列 {an} の各項の逆数を並べてできる数列が等差数列となっているので、数列 {an} は調和数列の定義を満たしています。
この例では、「もとの数列」と意識していましたが、文字を使った問題では、どちらが調和数列なのかと混乱しないことが大切になります。
落ち着いて定義に照らし合わせることで、初動で誤解をしないことが大切になります。
調和数列 :問題で練習
【練習問題】
調和数列 {an} の連続する三つの項の値が p, q, r だとします。(ただし、p, q, r は、どれも 0 ではない実数とします。)
このとき、q を p と r を用いて表してください。
こういうように、実際の問題で文字ばかりになっているときもあります。
定義に基づいて考察を進めることで、ミスなく答えに辿り着けることが多いです。
数列 {an} が調和数列ということなので、{an} の各項の逆数を並べてできる数列が等差数列ということになります。
p, q, r が連続する {an} の項なので、数列 {1/an} において、これらの逆数が、三つの連続する項となっています。
1/p, 1/q, 1/r は、数列 {an} が調和数列なので、数列 {1/an} は等差数列となっています。
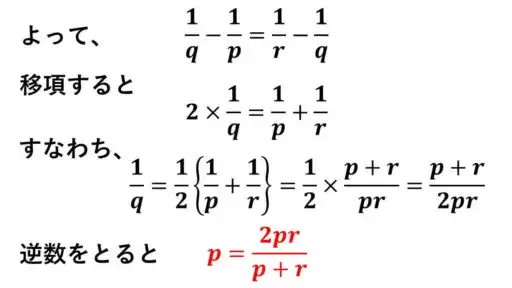
これで、q を p と r を用いて表すことができました。
数列 {an} と数列 {1/an} について、どちらが等差数列なのかを正しく認識することが大切になります。
練習にもう一つ問題です。
もう1題
【練習問題2】
4, 2, p, q が調和数列となっていたとします。(ただし、p, q は 0 でない実数です。)
このとき、p, q の値を求めてください。
4, 2, p, q が調和数列なので、
1/4, 1/2, 1/p, 1/q が等差数列となっています。
この等差数列の交差が具体的に計算できる状態です。
1/2 - 1/4 = 2/4 - 1/4 = 1/4 より、
交差が 1/4 です。
等差数列の交差は一定値なので、
p - 2 = 1/4, q - p = 1/4
まず、p の値から求めます。
p = 1/4 + 2 = 9/4 です。
p = 9/4 を使って、q の値を求めます。
q = 1/4 + p
= 1/4 + 9/4 = 10/4 = 5/4 です。
これで、q の値も求まりました。
こういった具体例を通じて、学習し始めたときに出てきた定義を確認すると、理解しやすいかと思います。
最後に、今回の内容の背後で使われている合成関数の考え方を述べておきます。
調和数列 :関数の合成
実数列は、各自然数 n に対して 実数 an を対応させています。
そのため、規則に基づいて実数を並べた数列が与えられることと、自然数全体を定義域とする実数値関数が与えられることが同値となっています。
第 n 項の値が実数 an ということを関数の言葉で述べると、「自然数 n に対して 実数 an が対応している」ということになります。
そのため、調和数列の定義に使われている合成関数の内容を述べておきます。
数列 {an} が与えられたときに、新しい数列 {1/an} を定義しています。
ここで、合成関数の考え方が使われています。
y = an という関数が数列です。自然数 n に対して、an を対応させる関数です。
y = an のグラフを xy-座標平面に描くと、
(自然数, 実数)という形の点たちとなっています。
ここで、関数の記号ですが、y = f(t) は、t の値に応じて y の値が、ただ一つ定まっているということです。
例えば、f(t) = 1/t だと、3 に対して 1/3 を対応させます。
ここで、t = g(n) とすると、自然数 n に応じて t の値が、ただ一つ定まるということです。
数列の記号では、g(n) という n に応じて定まる値のことを an と表記します。
n に応じて第 n 項の値 an を対応させるということです。
ここまでの内容を式で整理すると、
y = 1/t, t = an です。
この二つの関数を合成すると、定義域を自然数全体とする実数値関数 y = 1/an となります。
この関数が、数列 {1/an} です。
数列 {an} が 1, 1/2, 1/3, … という第 n 項が 1/n となっているときに、数列 {1/an} を考えました。
y = 1/t, y = an の合成関数で考えると、
y = 1/an です。
an = 1/n の逆数が y なので、y = n
これは、数列 {1/an} の第 n 項の値が n ということを表しています。
実は、数学2でも関数について、数学3の基礎となる内容が使われています。
今回は、逆数をとるということについて、調和数列を通じて合成関数の発想が使われていました。
ちなみに、恒等式の単元では、二つの関数が等しいという相当関係を学習しています。
また、関連する記事として、特殊な特性方程式を使う漸化式があります。
一次分数型の漸化式という記事で、知っておくと良い分数型の漸化式の解き方について解説をしています。
基礎的な等差数列の内容については、等差中項という記事で説明をしています。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。