部屋割り論法 (鳩の巣原理)| 少なくとも1つは

部屋割り論法 (もしくは鳩の巣原理)という誰もが納得しやすい命題を拠り所にして、条件を満たすものが少なくとも一つ存在するということを示す問題が高校の数学で扱われるときがあります。
難しい大学受験の問題だと、問題文の内容自体が複雑だったり、部屋割り論法以外の論点が難しいこともあるのですが、部屋割り論法自体は親しみやすい内容です。
表紙の図で述べているように、異なる 3 部屋に、4 人を配置しようとすると、2 人以上の人が入っている部屋が、少なくとも 1 部屋は存在することになります。
これを n を用いて一般的に、
n 室の部屋に (n+1) 人を配置しようとすると、2 人以上の人が入っている部屋が、少なくとも 1 室は存在するということになります。
これを部屋割り論法(鳩の巣原理)といいます。
それでは、シンプルな整数(自然数)を用いた例を通して、部屋割り論法を実際に使って論証を進める練習問題を解説します。
部屋割り論法 :必然的にあふれる数
<部屋割り論法の証明>
n 室に (n+1) 人を配置したとき、どの部屋も 1 人以下の人しか入っていなかったと仮定します。
すると、n 室の部屋に配置されている人数が、n 人以下ということになってしまいます。
これは、(n+1) 人を配置したことに矛盾します。
よって、背理法から、「n 室の部屋に (n+1) 人を配置しようとすると、2 人以上の人が入っている部屋が、少なくとも 1 室は存在する」ということになります。
では、具体的な例を使って、部屋割り論法を使う練習をします。
【部屋割り論法1】
1 以上 30 以下の整数から、相異なる整数を 16 個選びます。
このとき、選んだ 16 個の整数には、必ず 16 以上の整数が含まれます。
<証明>
1 以上 15 以下の整数の個数は 15 個です。
そのため、部屋割り論法から、16 個の選ばれた相異なる整数の中には、少なくとも一つは 16 以上の整数が存在することになります。【証明完了】
15 個までは、16 以上であるという条件に該当しないように選ぶことができます。しかし、必然的にあふれた 1 個は、16 以上 30 以下の整数となってしまうというわけです。
集合を使うと、次のように考察をすることができます。
1 以上 15 以下の整数全体を A とし、16 以上 30 以下の整数全体を B とします。
すると、A ∩ B は空集合で、
A ∪ B は 1 以上 30 以下の整数全体となります。
個数定理より、
n(A ∪ B) = n(A)+n(B)-0
= n(A)+n(B) = 15+15 = 30 となっています。
今、示した内容の表裏一体となる命題も証明できます。
表裏一体の事柄をどちらも証明
【部屋割り論法2】
1 以上 30 以下の整数から、相異なる整数を 16 個選びます。
このとき、選んだ 16 個の整数には、必ず 15 以上の整数が含まれます。
<証明>
16 以上 30 以下の整数の個数は 15 個です。
そのため、部屋割り論法より、
選んだ 16 個の中に、少なくとも一つは 15 以下の整数が含まれています。【証明完了】
先ほど示した内容と表裏一体となる内容も示しました。
図形的な考察を交えた内容も出題されるときがあるので、そういった内容を次に説明します。
部屋割り論法 :図形的な内容も考察
【練習問題】
正三角形ABCの各辺の長さが 4 だとします。
この正三角形の内部から相異なる 5 個の点を取ることを考えます。
このとき、取った 5 個の点のうち、少なくとも 2 点は距離が 2 以下になっていることを証明してください。
文章だけだと、難しそうなので、図を用いて考察を進めます。
正三角形ABCの内部は次の図のように4つの領域に分けることができます。
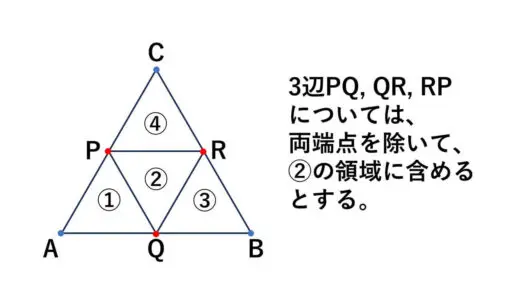
正三角形ABCの内部から点を取るので、3辺PQ, QR, RP については、両端点を除いて②の領域に含めるとしておきます。
この図のように、正三角形ABCは、各辺の長さが 2 となっている4つの正三角形に分かれます。
この図の内容と合わせて部屋割り論法(鳩の巣原理)を使うことを考えるわけです。
証明を開始
正三角形ABCの内部から相異なる 5 個の点を取ると、部屋割り論法により、少なくとも2個の点は①から④の中で同じ領域に含まれることになります。
ここで4つに分けている各辺の長さが 2 の正三角形に注目します。
例えば、正三角形AQPを見てください。
点 A 中心の半径 2 の扇形AQPの中に①の領域が収まっています。
そのため、①の領域の中から異なる 2 点をどのように取っても、その2点の距離は 2 以下ということになります。
同様に②や③や④の各領域について、その中から異なる2点をどのように取っても、その2点の距離は 2 以下になります。
以上の内容をまとめます。
正三角形ABCの内部から相異なる 5 個の点を取ると、少なくとも2点は①から④の中の同じ領域に含まれることになります。
そして、同じ領域に含まれた2点の距離は半径 2 の扇形の内部にある異なる2点のために、距離が 2 以下ということになります。
これで、部屋割り論法と図形的な内容を合わせた証明が完成しました。
異なる 5 個の点のうち、少なくとも2個は同じ領域の中に含まれてしまうというところが部屋割り論法の内容になります。
ちなみに、扇形については数学2でも扱われるので、関連する記事を投稿しています。
■ 扇形の弧の長さ
最後に、整数の内容との関連問題を扱います。
部屋割り論法 :整数との関連問題
【余りに関する証明問題】
整数 a, b, c, d を 3 で割った余りを、それぞれ p, q, r, s とします。
このとき、a, b, c, d から 2 個を選ぶ組合せの中で、少なくとも一つの組は、選んだ二つの整数の差が 3 の倍数となることを証明してください。
<証明>
整数を 3 で割ったときの余りは、0, 1, 2 の 3 種類しかありません。
そのため、部屋割り論法から、余りである p, q, r, s の中には重複している余りが存在することになります。
そこで、a, b, c, d の中から 3 で割ったときの余りが等しくなる二つの整数を選びます。
その選んだ二つの整数を x, y と置きます。
x と y を 3 で割ったときの余りが等しいので、その余りを r とします。(r は、0, 1, 2 のいずれかです。)
除法の原理(定理)より、ある整数 k, h を用いて、
x = 3k+r, y = 3h+r と表すことができます。
この x と y で差を計算すると、
x-y = (3k+r)-(3h+r)
= 3(k-h) となります。
k-h は整数なので、
3(k-h) は 3 の倍数です。
すなわち、x-y という選んだ二つの整数 x と y の差は、3 の倍数です。【証明完了】
余りについての整数問題で、部屋割り論法が絡むときがあります。
「n 人を n 個の部屋に入れるとき、どの部屋にも 1 人以上は入れないという条件のもとでは、n 人は 1 部屋に 1 人ずつ配置されることになる」というタイプの部屋割り論法も使われます。
抽象的な証明で、よく使う手を紹介します。
相異なるk個の余り
自然数 k で割ったときの余りで、
r1, r2, … , rk という k 個の非負整数があったとします。
そして、これら k 個の余りは、すべて相異なるという状況だったとします。
このとき、部屋割り論法から、
r1, r2, … , rk はそれぞれ、
0, 1, 2, … k-1 という k 個の余りに配置されることになります。
自然数 k で割ったときの余りは、0, 1, 2, … k-1 という k 個です。
これらを k 個の部屋だと思います。
r1, r2, … , rk を k で割ってできた k 個の相異なる余りを k 人の人だと考えて、部屋割り論法を使います。
すると、n 人は 1 部屋に 1 人ずつ配置されるということです。
この内容は、フェルマーの小定理の証明で使うことができます。
※ リンク先の記事は、大学で扱う環論の入門内容となっています。
小さい整数を使って、具体的に見てみます。
5, 6, 7 を k = 3 で割ったときの余りを
それぞれ r(5), r(6), r(7) と置きます。
一般に連続する 3 個の整数を 3 で割ったときの余りは、相異なります。
そのため、r(5), r(6), r(7) は、相異なる 3 で割ったときの余りです。
3 で割ったときの余りは、0, 1, 2 の 3 種類しかありません。
r(5), r(6), r(7) を、
部屋0、部屋1, 部屋2 に配置することを考えます。
部屋割り論法より、
r(5), r(6), r(7) は重複することなく相異なる部屋に配置されます。
実際に計算して確かめてみます。
5÷3, 6÷3, 7÷3 の余りは、それぞれ 2, 0, 1 なので、
r(5) = 2, r(6) = 0,
r(7) = 1 となっています。
r(5) は部屋2 に、r(6) は部屋0 に、r(7) は部屋1 に配置されています。
確かに重複なく、どの部屋にも 1 人ずつ入っています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。