実部と虚部 – 比較 | 高校の典型的な問題の後で大学の代数の内容に言及
" 実部と虚部 – 比較 “について、高校で学習する典型的な問題について解説をします。
基礎的な計算問題の類いは、高校で学習する教科書の例題で扱われる解き方を押さえておくとスムーズに得点をすることができるかと思います。
しかし、よくよく考えてみると、いはゆる教科書レベルの問題は解けるのだけれども、複素数についての根本となる代数構造が分からないということが起きるかもしれません。
そこで、はじめに高校数学の典型的な内容を解説した後で、大学の代数学につながる内容を述べています。
この記事の最後の方で述べる代数学の内容は、高校生の方からすると難しい内容になるかもしれません。
しかし、大学の数学科の内容を知っている方からすると、高校のレベルで扱える実数体上の2次元の可換結合代数の具体例となっています。
実部と虚部 – 比較 :高校で習う典型的なもの
a+bi (a, b は実数) は、虚数単位 i とした1つの複素数です。
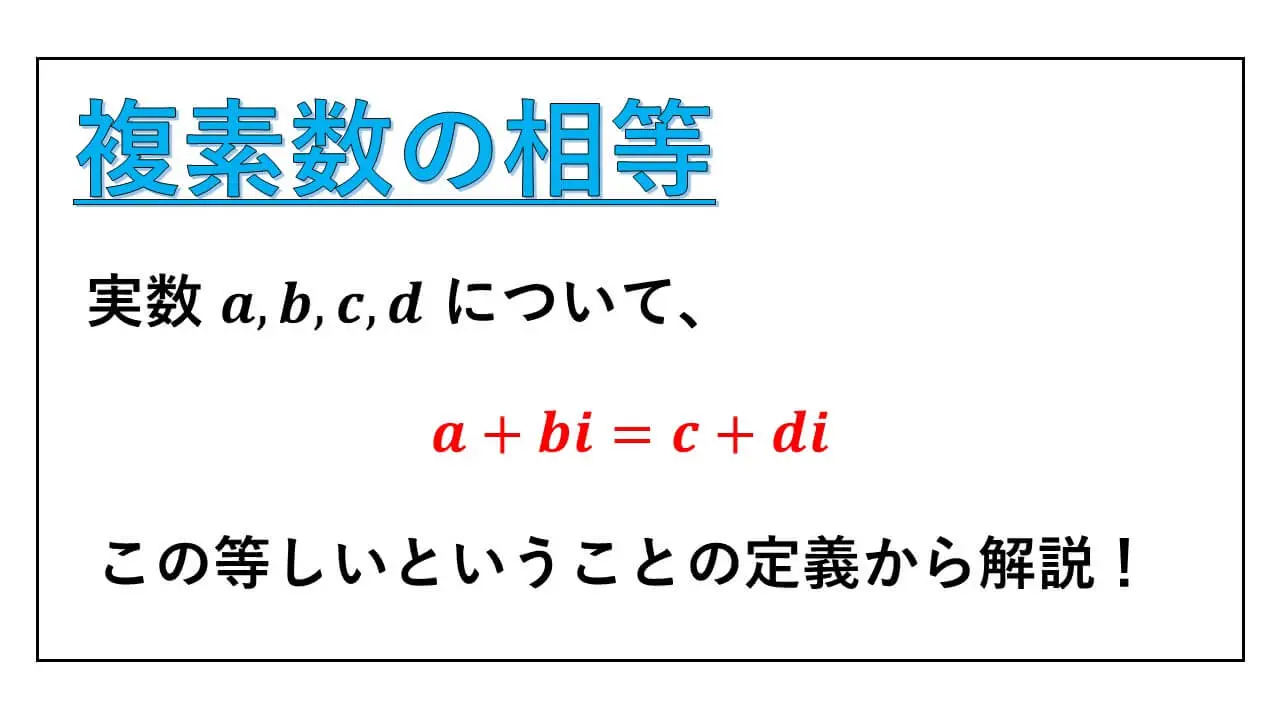
複素数が2つ与えられたときに、「等しい」ということが定義されています。
この2つの複素数が等しいということを複素数の相等といいます。
【複素数の相等の定義】
a, b, c, d を実数とする。
a+bi, c+di という二つの複素数について、次のときに限り、これら二つの複素数が等しいと定義する。
つまり、
a = c かつ b = d のときのみに限り、これら二つの複素数が等しいと定める。
また、a+bi と c+di が等しいとき、
a+bi = c+di と表す。
実部どうしが等しく、なおかつ虚部どうしが等しいときに、二つの複素数が等しいというのが定義です。
この定義に基づいて、二つの複素数が等しいか等しくないのかを判断します。
複素数を数学2で学習し始めたときに出てくる問題を通して、複素数の相等の定義を使ってみます。
s, t を実数とし、
s+5i = 3+ti とします。
このとき、実数 s と t の値を求めてみます。
複素数の相等の定義から、
s = 3 かつ 5 = t です。
すなわち、
s = 3, t = 5 となっています。
この様に、実部どうしと虚部どうしを比較して考えます。
次に、もう少し複雑なタイプの問題を扱ってみます。
論理を使う数2の典型問題
【典型問題】
複素数 z が、z2 = 32i を満たしたとします。
このとき、z の値を求めてください。
この右辺の 32i は、正確に述べると、
0+32i です。
実部が 0 で、32 が虚部です。
0 を足しても値は同じままなので省略されますが、複素数の相等の定義を考えるときには、実部と虚部の値をどちらも認識することになるので注意です。
次に、z = a+bi (a, b は実数) が、
z2 = 32i を満たしたとして実数 a と b の値を決定します。
z2 = (a+bi)2 の実部と虚部を明確に認識できる形に、計算を進めて式を書き換えます。
z2 = a2+2abi+(bi)2
= (a2-b2)+2abi です。
z2 = 32i より、
複素数の相等の定義から、
a2-b2 = 0 かつ 2ab = 32 です。
すなわち、
(a+b)(a-b) = 0 かつ ab = 16 です。
ここで、数学の論理を使います。
0 でない実数 x と 0 でない実数 y で乗法を計算すると、その積 xy は 0 でない実数です。
この対偶をとると、
二つの実数の積 xy が 0 だと、
x = 0 または y = 0 となります。
今、a+b, a-b はどちらも実数なので、
積 (a+b)(a-b) = 0 より、
a+b = 0 または a-b = 0 ということになります。
つまり、
a = -b または a = b という状況です。
ab = 16 だったので、場合分けをして b の値を決定します。
【a = -b の場合】
このとき、
16 = ab = -b2 となります。
つまり、b2 = -16 < 0 です。
しかし、b は実数なので、
b2 ≧ 0 でなければなりません。
b2 ≧ 0 と b2 < 0 が同時に成立しているため、矛盾です。
よって、a = -b という場合は起きないという結論になります。
【a = b の場合】
このときは、
16 = ab = b2 となっています。
そのため、b = 4 または b = -4 です。
よって、
b = 4 の場合は、
a = 4 で、
b = -4 の場合は、
a = -4 です。
以上より、
z2 = 32i を満たす複素数 z は、
z = 4+4i, -4-4i の二つとなります。
実部どうし、虚部どうしを比較するという複素数の相等についての典型的な問題を扱いました。
高校の数学では論理が絡むので、落ち着いて論理的な考察を進めることに慣れておくと良いかと思います。
ここからは、大学の代数学の内容に触れておきます。
実部と虚部 :2次元の可換結合代数の例へ
ここから使う記号ですが、実数全体を R と表すことにします。
この R は、通常の実数の加法と乗法について可換体となっています。
そして、
xy-座標平面上の点 (0, 0) を始点として、座標平面上の各点を終点とする平面ベクトルをすべて集めた集合を S とします。
つまり、
{(a, b) | a, b∈R} という実数を成分とする平面ベクトル全体を S とします。
この S における二項演算を二つ定義します。
※ 四則演算という記事で数学科で扱う内容を見据えた基礎的な内容を解説しています。
そして、R からのスカラー倍も定義します。
S×S → S を、
(a, b), (c, d)∈S に対し、
(a, b) + (c, d)
= (a+c, b+d)∈S と定義します。
これは、高校のベクトルの単元で学習する平面ベクトルどうしの加法です。
そして、r∈R から、
(a, b)∈S への作用を、
r(a, b) = (ra, rb) と定義します。
これも、平面ベクトルのスカラー倍です。
この加法とスカラー倍について、S はベクトル空間の公理を満たします。
線形代数学の言葉を使うと、
(1, 0) と (0, 1) という二つの平面ベクトルが S の基底となっています。
基底を構成する要素(元)の個数が2個なので、2次元のベクトル空間(線形代数)ということです。
線形代数に乗法を定義する
大学の数学科では、1年のときに線形代数学を学習します。
そして、2年や3年のときに、
代数(algebra)というものを学習します。
これは、線形代数(加群)に乗法を定義した数学的な構造となります。
先ほどの実数を x 成分と y 成分とする平面ベクトル全体 S は線形代数(ベクトル空間)なので、さらに乗法を定義することで代数の構造を与えます。
加法とは異なる S における二項演算である乗法を定義します。
(a, b), (c, d)∈S に対し、
(a, b)(c, d)
= (ac-bd, ad+bc)∈S と定義します。
※ この乗法は、外積とは違った二項演算です。
正確に確認すると記述量が長くなりますが、乗法の定義に基づいて計算をすることで、交換法則と結合法則と分配法則が成立していることが分かります。
この乗法について、
(1, 0)∈S が乗法単位元となります。
(1, 0)(a, b) = (a, b),
(a, b)(1, 0) = (a, b) となることが S における乗法の定義から分かります。
また、(a, b) ≠ (0, 0) のとき、
(a, b)(a, b)-1 = (1, 0) を満たす乗法逆元(逆数)である (a, b)-1 が存在することも導かれます。
この S における加法と乗法という二つの二項演算と実数体 R からのスカラー倍について、S は可換結合代数となっています。
乗法について交換法則と結合法則が成立することから"可換結合"である代数ということです。
表面的な記号の変更
S は高校の数学で学習する実数成分の平面ベクトル全体でしたが、高校では学習しない乗法を定義することにより、実数体上の2次元の可換結合代数となりました。
さらに、スカラー倍のことを忘れると、加法と乗法について、S は可換体の定義も満たしています。
ここで、表面的な記号を変更することにします。
(a, b)∈S のことを、
a+bi と記述することにします。
この第二成分の部分が b ということを表すのに用いたアルファベット i が虚数単位です。
S における加法は、
(a+bi)+(c+di)
= (a+c)+(b+d)i です。
(a, b)+(c, d)
= (a+c. b+d) を表面的に記号を変えただけです。
乗法についても、
(a+bi)(c+di)
= (ac-bd)+(ad+bc)i です。
(a, b)(c, d)
= (ac-bd, ad+bc) の表面的な記号の変更です。
この a+bi という表面的な記号を変更したもの全体を C と表すことにします。
つまり、
{a+bi | a, b∈R} が C です。
この C の要素(元)のことを高校の数学では複素数といっていたわけです。
実数体上の2次元の可換結合代数 C です。
可換結合代数は大学の数学科の2年か3年で出てきますが、その具体例を高校の段階から知っているので、心強いです。
ガウスの時代には、線形代数はまだ知られていなかったので、複素数は得体の知れないものでしたが、現代の数学ではその存在は、上で述べたように明確なものです。
実数を成分とする平面ベクトルに乗法を定義したものに過ぎませんから、複素数の存在を疑うことは今日ではありません。
それよりも、抽象的な複素数を学習するときに、示しておかなければならないことは、乗法逆元の存在です。
ちゃんと計算過程を述べると長くなりますが、
(a, b) ≠ (0, 0) のときに、
(a, b)-1 という乗法逆元(逆数)が存在することは、理解しておく必要があります。
関連する記事として、
虚数と複素数の違いという記事も投稿しています。
集合を用いた議論に慣れることを目的に、敢えて大学の数学を意識した集合の記号を用いて議論を進めています。
表面的な記号の違いはありましたが、二つの複素数が等しいのか等しくないのかということは、議論を進める上で押さえておくべき定義となります。
最後にまとめておきます。

これで、今回の記事を終了します。
読んで頂き、ありがとうございました。