浮動小数点数 | バイアス値15の半精度で高校の情報を学習
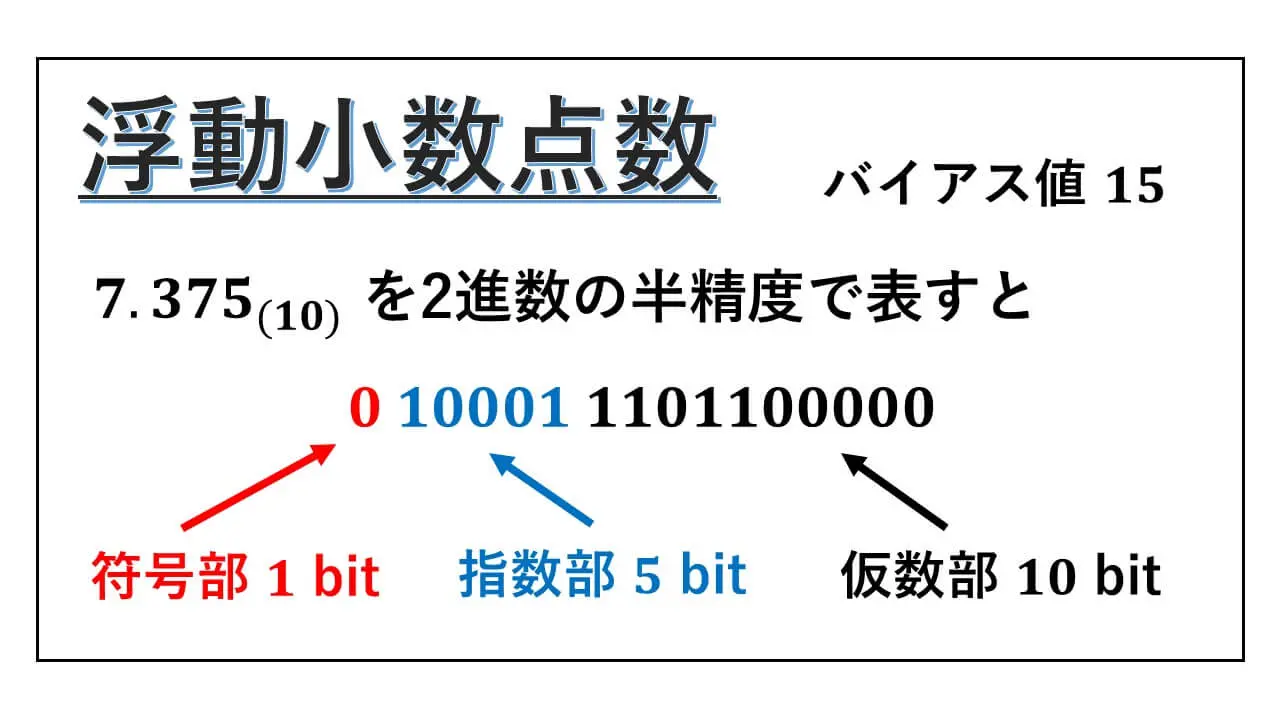
" 浮動小数点数 “について、高校の情報で扱われる" バイアス “値15の半精度の内容を解説しています。
IEEE754で規定されている浮動小数点数を、高校数学の計算と併用して学習を進められるように説明をしています。
※ アイトリプルイーと読みます。
符号部、指数部、仮数部を用いた表し方をどのように決めているのかを、ていねいに把握することが大切になります。
学習の始めに、桁数が小さい方が良いだろうということで、16ビットの半精度の内容を取り挙げています。
それでは、具体的な数字を使って、2進数の半精度の浮動小数点数で表すことについての解説から始めます。
浮動小数点数 – バイアス :具体例で内容を理解
【2進数についての半精度】
・符号部は正のプラスが 0 で、負のマイナスは 1 と表す。
・指数部については、バイアス値15を使う。
・仮数部は常に 1 となる最高位の数を省略し、2番目の数からとする。
符号部は 1 ビット、指数部は 5 ビット、仮数部は 10 ビットとなる。
大雑把な2進数の半精度の浮動小数点数にするときのポイントになります。
これから、7.375という10進数の数を2進数の半精度の浮動小数点数で表すことについて、詳しく細部を説明します。
2進数で考えたいので、7.375を2進数の小数に直します。
※ 5進数の小数という記事でn進法の小数について解説をしています。
7.375 は、
4+2+1+0.25+0.125 なので、
111.011(2) という2進数の小数です。
この 111.011(2) は固定小数点数での表し方です。
これを浮動小数点数に直す方法について、これから述べます。
111.011(2) は、
+1.11011×22 と捉えます。
2 を1つ掛けると、小数点が左に 1 移動します。
+0.111011×23 と同じ値と認識します。
反対に2-1を1つ掛けると、小数点が右に1移動します。
23×2-1は22で、小数点が右に1移動し、
+1.11011×22 となります。
+1.11011×22 は正の数なので、符号部の値は 0 ということになります。
この形から、符号部と指数部と仮数部の値が得られます。
22と基数である2の指数が 2 となっています。
この指数の 2 にバイアスがかかり、指数部の値となります。
バイアス値15を加える
2進数の半精度の浮動小数点数は、バイアス値が 15 となっています。
+1.11011×22 という形の指数に 15 を加えます。
2+15 = 17 となります。
半精度だと、必ず 15 を加えるという規定です。
半精度の他にも単精度など他の浮動小数点数の表し方もあります。
単精度だと、かかるバイアス値は127となります。
この記事では、半精度について述べるので、指数部を考えるときのバイアスは 15 としています。
今、2+15 = 17 としたのですが、こうして得られた値は10進数です。
そのため、この17を2進数に直し、その値を指数部の値とします。
17 = 16+1
= 1・24+1・20 より、
10001(2) です。
これで、
+1.11011×22 の指数部が、
10001 と分かりました。
7.375という10進数の小数を2進数の半精度の浮動小数点数で表すと、符号部の値が 0 ということは先ほど述べました。
残すは、仮数部の値です。
仮数部の値
7.375は、
111.011(2) でした。
これを、
+1.11011×22 という形で捉えたのは、仮数部について、常に 1 となる最高位の数を省略し、2番目の数から表すからです。
そのため、2の何乗かを掛けることで小数点の位置を移動させ、最高位の数を 1 にしたわけです。
今回は、22を掛ける形にすることで、
+1.11011×22 と最高位の数を 1 にできました。
この形にしてから、小数部の値をそのまま並べます。
ただし、通常の小数では末尾の永遠に続いている 0 は省略されていますが、仮数部が10ビットということを考慮しなければなりません。
11011という小数部の数は 5 桁ですが、10ビットで表すので、残りの 5 桁は省略されていた 0 を表示させた形にします。
つまり、右側に 0 を 5 個つぎ足すわけです。
よって、
1101100000 が仮数部の値となります。
これで、
7.375(10) = 111.011(2) を半精度の浮動小数点数にすると、次のようになることが分かりました。
すなわち、
0 10001 1101100000 です。
符号部が 0 で
指数部 10001 で
1101100000 が仮数部です。
逆算して、もとの小数を求めることもできます。
符号部が 0 なので、正の数だと分かりますし、指数部からバイアス値が加わる前の指数も分かります。
10001(2) が指数部だと、
1・24+1・20 = 17 がバイアス値を加えた後の値です。
そのため、
17-15 = 2 が、バイアス値15を加える前の指数の値です。
仮数部の右につぎ足した 0 を消すと小数部です。
20の位は常に 1 だったことと合わせると、
1101100000 だから、
+1.11011×22 です。
つまり、
111.011(2) が、もとの2進数の小数だと、逆算できるわけです。
次に、もとの小数が分かるということを利用して、浮動小数点数で表された数の足し算(引き算)を考えてみます。
浮動小数点数で表された数の計算

X や Y が、どういう2進数の数かを押さえておきます。
逆算するときに、指数部の2進数から、バイアスがかかる前の10進数で表される指数を押さえることが大切になります。
X の指数部は、
10010(2) なので、
1・24+1・21
= 16+2 = 18 と考えます。
これはバイアス値15を加えた後の値なので、18から15を引くと、もとの指数の値となります。
18-15 = 3 です。
X の符号部は 0 で、正の数というのが分かります。
さらに、仮数部の右に連なる 0 を省略し、
20の位が常に 1 より、
X = +1.1101×23と分かります。
Y の方は、符号部が 1 なので負の数です。
指数部が10001より、
同様にして、
1・24+1・20
= 16+1 = 17 からバイアス値15を引いて指数の値を得ます。
17-15 = 2 が指数の値です。
仮数部より、
Y = -1.1001×22となっています。
X = +1.1101×23,
Y = -1.1001×22 について、
X+Y を計算するということになります。
ここで、基数2の指数が異なっているので、係数どうしをそのまま計算することができません。
そのため、まずは小数点を移動させることで、基数2の指数を揃えます。
このときに、大きい方の指数の値に揃えます。
今回は、X の方が大きいので、指数を 3 に揃えます。
Y の方の小数点を左に1動かし、21を掛けるという変形をすると、指数が 3 に揃います。
Y = -1.1001×22
= -0.11001×23 です。
よって、
X = +1.1101×23 と
Y = -0.11001×23 で、
X+Y を計算することになります。
ここで、分配法則が役に立ちます。
X+Y は、23でくくり出すと次のようになります。
つまり、
(+1.1101-0.11001)×23 が求める値です。
後は、括弧の中の2進数の引き算をすれば良いわけです。
+1.1101(2)-0.11001(2)
= +1.00001(2) となります。
よって、
+1.00001×23 で、×23は小数点を右に 3 移動させるということなので、
1000.01(2)が求める値です。
この内容をコンピュータが行うためには、0 と 1 で操作を表さなければなりません。
そこで、浮動小数点数で表された状態のまま、実行する方法も押さえておきます。
0と1で導く
X の指数部 10010 は、
Y の指数部 10001 よりも大きいので、大きい X の方の指数に揃えるということでした。
10010(2)と10001(2)の2進数における差は 1(2) です。
そのため、指数の値の差が 1 ということです。
ということは、小数点の位置を 1 つだけ移動させるということになります。
先ほどの計算で21を掛けて揃えた部分の操作を 0 と 1 で表現することを考えます。
10ビットの Y の仮数部の数字を一斉に右へ 1 だけズラします。
一番右の 0 は10ビットから外れるので、その 1 つの 0 は無視します。
注意点は、20の位の 1 がスライドしてきて、1番左に出てくることです。
これらを踏まえ、
Y の仮数部を次のように変化させます。
つまり、
1001000000 だったのを、
1100100000 へ変化させます。
こうしておいてから、
Y は負の数なので、
X の仮数部の値と、
今の1100100000で引き算をします。
つまり、
1101000000
-1100100000 という2進数の足し算を計算します。
すると、
0000100000 となります。
これが、X+Yの仮数部の値です。
X+Y は正の数のままなので、符号部の値は 0 です。
X の方の指数に揃えたので、
X+Y の指数部は、X と同じ値です。
つまり、
10010 が X+Y の指数部の値です。
まとめると、
0 10010 0000100000 が、
X+Y の2進数の半精度の浮動小数点数における表し方です。
これを通常の2進数で表してみます。
+1.00001×23 です。
×23は小数点を右に 3 移動させるということなので、
1000.01(2)と先ほどの計算と同じ値になっています。
コンピュータとのやり取りなので、×23のようなことを 0 と 1 だけで表すということから、このような浮動小数点数のままでの計算も考えるというわけです。
参考までに
今回の記事で扱ったのは、半精度の浮動小数点数でした。
半精度だと、
符号部は 1 ビット、指数部は 5 ビット、仮数部は 10 ビットで、全体が 16 ビットです。
そして指数部に関して、バイアス値15でした。
単精度浮動小数点数だと、
符号部は 1 ビット、指数部は 8 ビット、仮数部は 23 ビットで、全体が 32 ビットとなります。
このときは、バイアス値が127になります。
指数の値に127を足してから、2進数にして指数部にするので、今回の記事よりも多くの桁数で計算をすることになります。
また、仮数部の値が23桁なので、全体の桁数が多いです。
さらに、倍精度浮動小数点数という全体で128ビットの表し方もあります。
こうしたことから、計算の分かりやすさを狙って、学習のはじめに半精度浮動小数点数を扱いました。
高校の情報の内容以外の記事も投稿していまして、コンピュータ絡みで数式の入出力についての記事もあります。
分数指数-コード入力という記事では、数学の数式を出力する命令文について述べています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。