第n項までの和 Sn | もとの数列の一般項を定める規則との関係を理解する【和を求めるΣ】

2023年9月10日

第 n 項までの和 S_n は、数列の一般項を定める規則を用いて定義されています。

記事の後半では、和の最大についての内容も、述べています。

また、第１項から第 n 項までの和なので、シグマについての公式を利用できるときがあります。

既に学習した内容を利用して、数学Bで学習する数列の和について解説しています。

基礎をしっかりと理解すると、
n ≧ 2 のときに、
S_n－S_n-1 = a_n という公式が自然と理解できます。

それでは、S_n の定義から解説をします。

第n項までの和 :Snの定義

数列 {a_n} が与えられているときに、それぞれの自然数 n に対して、値を対応させることができます。

その対応させる値を S_n と表すことにし、
S₁ = a₁,
n ≧ 2 に対しては、
S_n = a₁+a₂+…+a_n と定義します。

これで、どの自然数 n に対しても、S_n という値を対応させることができました。

自然数 1 に対応する値 S₁ は、数列 {a_n} の第 1 項の値 a₁ です。

2 以上の自然数 n については、数列 {a_n} の第 1 項から第 n 項までに現れている各項の値たちを全て足し合わせた値を S_n と定義しています。

n ≧ 2 のとき、
a₁+a₂+…+a_n は既に学習したシグマ記号を用いて表すことができます。

a₁+a₂+…+a_n = Σ_k a_k です。

この添え字の k は、1 以上 n 以下の範囲にある自然数で、1 から n まで動きます。

そのため、n ≧ 2 のとき、
S_n = Σ_k a_k となっています。

この等式は、S_n の定義をシグマ記号を使って書き換えたものになります。

シグマ記号には、公式がいくつかあるので、それらの公式が使えるときがあります。

● Σ_k k = 1/2 × n(n+1)
● Σ_k k² = 1/6 × n(n+1)(2n+1)
● 定数 p のとき、Σ_k p = pn

このようなシグマ記号についての公式を使えるときは、第 1 項から第 n 項までの和という抽象的な定義を具体的に計算で求めることができます。

この S_n の定義は、既に与えられている数列 {a_n} の各項の値を用いることで、新しい数列 {S_n} を定義しています。

数学IIIでは、この数列 {S_n} を部分和と呼び、極限操作を使って、無限級数の収束や発散を議論するのですが、この記事は数Bの範囲に限定をして解説をしています。

ここからは、具体的な例を使って、S_n がどうなっているのかを観察します。

具体例で一般項との関係を見る

a_n = 2n+3 を一般項とする数列 {a_n} を使って、数列 {S_n} の第 n 項の値を n を用いて表します。

{a_n} の第 1 項の値は、
a₁ = 2×1+3 = 5 となっています。

一般項が n の式で表されていると、具体的な項の値が計算で求めることができます。

{a_n} の第 2 項や第 3 項の値は、それぞれ次のように計算することができます。

a₂ = 2×2+3 = 7,
a₃ = 2×3+3 = 9 となっています。

では、各自然数 n について、S_n の値がどうなっているのかを定義に基づいて確認します。

S₁ = a₁ = 5 です。

自然数 1 に対応する値 S₁ は、a₁ と定められているので、{a_n} の第 1 項（初項）である 5 となります。

次に、n ≧ 2 の場合について、S_n の値を求めます。

S_n = a₁+a₂+…+a_n
= Σ_k a_k = Σ_k (2_k+3)

この k は 1 から n までの自然数を動くのですが、{a_n} の一般項を定めている規則となっている式が役に立ちます。

一般項が 2n+3 という式なので、
1 ≦ k ≦ n に対して、
a_k = 2k+3 です。

そのため、
S_n = Σ_k a_k = Σ_k (2_k+3) …(1)

ここで、シグマについての公式を使うチャンスです。

Σk (2k+3) = 2Σ_k k + Σ_k 3

3 は定数なので、Σ_k 3 は 3 を n 個足し合わせた値で、3n です。

そのため、
Σ_k=1n (2k+3)
= 2Σ_k=1n k +Σ_k=1n 3
= 2 × n(n+1)/2+3n
= n²+4n …(2)

(2) を (1) に代入すると、
n ≧ 2 のとき、
S_n = n²+4n です。

S₁ = 5 は、a₁ = 5 と一致しています。

n ≧ 2 のときだと、
例えば n = 3 のとき、
a₁+a₂+a₃
= 5+7+9 = 21 です。

S₃ を (2) の式で計算します。

S₃ = 3²+4×3 = 21 です。

確かに、
S₃ = 21 = a₁+a₂+a₃ となっています。

今度は、逆に S_n から数列 {a_n} の一般項の式を求めることを考えます。

第n項までの和 :Snから元の数列の一般項へ

数列 {a_n} の第 1 項から第 n 項までの和 S_n が次のようになっていたとします。

S₁ = a₁ = 5,
n ≧ 2 のとき S_n = n²+4n です。

このとき、{a_n} の一般項 a_n の値を n の式で表すことができます。

n = 2 の場合、
S₂ = a₁+a₂ です。

また、n－1 = 1 より、
S₁ = a₁ です。

そのため、
S₂－S₁ = (a₁+a₂)－a₁
= a₂

一方、
S₂－S₁ = (2²+4×2)－5
= 4+8－5 = 7

そのため、
a₂ = 7 … (1)

n ≧ 3 の場合を考えます。

Sn の定義から、
S_n = a₁+a₂+…+a_n-1+a_n

また、n－1 ≧ 2 より、
S_n-1 = a1+a2+…+a_n-1

ゆえに、辺々引くと、
S_n－S_n-1 = a_n …(2)

一方、k ≧ 2 のとき、
S_k = k²+4k だから、
k として、n, n－1 を考えると、
S_n = n²+4n,
S_n-1 = (n－1)²+4(n－1)
= n²+2n－3 です。

辺々引くと、
S_n－S_n-1
= (n²+4n)－(n²+2n－3)
= 2n+3 …(3)

(2), (3) より、
a_n = 2n+3 です。

n = 2 を代入すると、
2×2+3 = 7 です。

(1) より、a₂ = 7 だったので、
a_n = 2n+3 は、n = 2 の場合にも成立しています。

よって、n ≧ 2 の場合、
a_n = 2n+3 です。

ここまでの議論で、
n = 1 の場合には触れていません。

そのため、n = 1 のときにも、
a_n = 2n+3 の等式が成立するのかを検証しなければなりません。

2×1+3 = 5 で、a₁ = 5 だから、
n = 1 のときにも、
a_n = 2n+3 が成立しています。

nが1のときの注意点

この例では、n = 1 のときにも成立しましたが、n = 1 のときに成立しないことも起こり得ます。

n = 1 のときに成立しないときは、「n = 1 の場合には成立しない」と述べ、別途、a₁ として S₁ の値を記述します。

以上より、どんな自然数 n についても、
a_n = 2n+3 が成立しています。

たいていの高校数学Bの練習問題では、n が 1 のときにも成立する内容になっていますが、難しい大学受験の問題などで、n が 1 のときに成立せず、別途、a₁ を記述するときもあります。

ここまで、具体的に数列 {a_n} の一般項を与える規則である n の式を用いて S_n を定義することと、逆に S_n の値から a_n の値を求めることを述べました。

先ほど求めた {a_n} の一般項を用いて、他の数列を定義することができます。

各自然数 n に対して、
b_n = (a_n)² = (2n+3)² と定義します。

今度は、
b_n = 4n²+12n+9 を一般項とする数列 {b_n} の第 1 項から第 n 項までの和を S_n として、S_n の値を n を用いて表すことを考えます。

数列 {b_n} は、
5², 7², 9², 11², … という数列です。

第 1 項から第 n 項までの和を求めるときに、シグマの公式を使う良い練習問題かと思います。

第n項までの和 :練習問題

数列 {b_n} の一般項が、
b_n = 4n²+12n+9 だとします。

このとき、{b_n} の第 1 項から第 n 項までの和 S_n を求めてください。

b₁ = 4×1²+12×1+9
= 4+12+9 = 25 です。

そのため、S₁ = b₁ = 25 です。

次に、n ≧ 2 の場合を考えます。

1 ≦ k ≦ n である自然数 k について、
b_k = 4k²+12k+9 です。

そのため、
S_n = b₁+b₂+…+b_n
= Σ_k (4k²+12k+9)
= 4Σ_k k²+12Σ_k k+Σ_k 9

シグマについての公式を使って、S_n の値を計算します。

公式を用いて計算

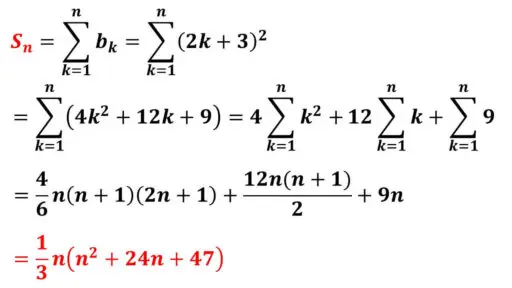
シグマの公式を使うことで、第 1 項から第 n 項までの和が求まりました。

このように、S_n の定義に a_n の一般項を定める規則である n の式が使われていて、シグマについての公式を使うことで、S_n も n の式で表せるときがあります。

この第 n 項までの和を求めるという観点で、等差数列の和の公式をもう一度見返してみると、より理解が深まるかもしれません。

ここからは、第n項までの和の最大について、数列の取る値をグラフで表したものも利用して話を進めます。

第n項までの和 :和の最大

「和の最大」という内容ですが、算数以来の数学の常識が使われています。

それは、正の数を加えると、合計値が大きくなるということです。

2+3 という数があったとします。

7 という正の数を、さらに加えた合計が、もとの数よりも大きくなるということを見てみます。

2+3 < (2+3)+7 となります。

正の数を加えたことによって、合計値が大きくなりました。

ここからは、和が最大となることを考えます。

最大ということは、和が小さくなるという状況も考えるわけです。

和が小さくなる原因として、負の数を加えるということが挙げられます。

中学一年で学習した負の数を加えると、和が小さくなることを見てみます。

2+3 に負の数 －4 を加えてみます。

2+3 > (2+3)+(－4) です。

この負の数を加えると、合計値が小さくなってしまうということが、最大性に関わってきます。

具体的な数字を使って、等差数列のときについて、和の最大を考えてみます。

初項から第何項までの和が最大か

自然数 n について、
a_n = 5－2(n－1) という初項 5、交差－2 の等差数列について和の最大を考えてみます。

a_n = －2n+7 が一般項です。

n に数を具体的に当てはめることで、各項の値を求めることができます。

a₁ = 5, a₂ = 3, a₃ = 1 と、第 3 項まで項の値を求めました。

ここまでは、正の数なので、
a₁ < a₁+a₂,
a₁+a₂ < a₁+a₂+a₃ となっています。

次に、第 4 項の値も考えてみます。

a₄ = －1 と負の数になっています。

負の数を加えることになるので、
a₁+a₂+a₃+a₄ の値は、
a₁+a₂+a₃ よりも小さくなります。

第 5 項以降も、ずっと負の数が続きます。

これで、初項から第 3 項までの和が最大ということが分かりました。

a₁+a₂+a₃ = 5+3+1 = 9 が、最大値ということになります。

他の求め方について

他の求め方についても述べておきます。

第何項までの和が最大になるのかということなので、初項から第 n 項までの和を n を使って表すことを考えます。

まさに正攻法な考え方になります。

そのため、この方法は、ぜひ押さえておく必要があります。

ただし、問題によっては楽に答えを出せるときもあるので、S_n を n で表すということまでしなくても良いときもあります。

問題の状況によって、S_n を考えるかどうかは、毎回の判断が大切になるので、日頃から判断の練習をしておくと良いかと思います。

では、S_n をシグマ記号を使って求めます。

初項から第 n 項までの和 S_n の求め方の基本はシグマ計算です。

S_n = Σ_k a_k で、k を 1 から n まで走らせます。

a_k = －2k+7 について、シグマの公式を使うと次のようになります。

S_n = ∑_k (－2k+7)
= －2∑_k k +∑_k 7
= －2×n(n+1)/2+7n
= －n²+6n

この S_n = －n²+6n が第n項までの和で、n を変数とする二次関数の式です。

ただ、n は自然数を動くので、定義域は自然数全体となっています。

n² の係数から、グラフの概形は上に凸ということが分かります。

平方完成をして、グラフについての情報を押さえます。

S_n = －n²+6n
= －(n－3)²+9

これで、n = 3 のとき、最大値が 9 ということが分かりました。

すなわち、初項から第 3 項までの和が最大で、その最大値が 9 ということです。

S_n を n を用いて表すことができると、様々な考察ができます。

しかし、シグマを使って求めるのは、結構な労力と時間を使います。

問題によっては、そこまでしなくても良いときがあるので、問題によっては時間短縮を考えることも大切かと思います。

このことに注意して、次の練習問題を考えます。

第n項までの和 :グラフを用いた考察

【練習問題】

自然数 n について、
a_n = －n²+6n－4 を一般項とする数列 {a_n} が与えられたとします。

この数列は、初項から第何項までの和が最大となるのかを求めてください。

もちろん、S_n を n を用いて表すことが重要になる問題もあります。

そのときに、シグマ計算が大変でも計算を正確にし続ける力も大切になります。

∑_k (－k²+6k－4) を、k が 1 から n までで走らせると S_n になります。

ただ、今回の練習問題では、そこまでしなくても楽に答えが求まります。

短い時間で楽に問題を解くということで、グラフのイメージを利用した解き方を説明します。

数列が与えられると、関数を定義することができます。

自然数 n に対して、数列の第 n 項の値を対応させるという関数が得られるからです。

1 という自然数に対応する数は、第 1 項の値です。

その値は、一般項の n の式に、
n = 1 を代入することで得られます。

a₁ = －1²+6・1－4
= 1 となっています。

数列から得られる関数のグラフは、(n, a_n) を座標とする点を打つことで、座標平面に表すことができます。

(1, 1) という点を座標平面に打つことになります。

a_n = －n²+6n－4 は、自然数全体を定義域とする二次関数の式となっています。

平方完成をすると、対称軸が見えます。

a_n = －(n－3)²+5 です。

n = 3 が軸で、
点 (3, 5) が頂点の座標です。

定義域が自然数全体ということで、つなげっていない点たちの集まりのグラフですが、二次関数の放物線上にある点たちです。

グラフを利用して押さえる情報は、「和が小さくなる原因である負の数」が出現するところです。

負の値の項を追う

グラフから、第 6 項に初めて負の値が出現するということが分かりました。

a₁ から a₅ までは全て正の値です。

そのため、
a₁ < a₁+a₂,
a₁+a₂ < a₁+a₂+a₃ というように、第 5 項までは項数を増やして和を取ると次第に合計の和は大きな値となっていきます。

a₁+a₂+a₃+a₄+a₅ で、和が最大となります。

a₆ = －4 は負の数なので、加えると合計の和は小さくなります。

二次関数のグラフの概形から、第 7 項以降の値もすべて負の数です。

そのため、初項から第 5 項までの和が最大ということになります。

最大和を確認

a₁ = 1, a₂ = 4, a₃ = 5,
a₄ = 4, a₅ = 1 です。

二次関数のグラフは軸について対称なので、a₄ = 4, a₅ = 1 は計算をしなくても値が分かります。

これで、
a₁+a₂+a₃+a₄+a₅
= 1+4+5+4+1
= 15 と最大の和の値が確認できました。

問題によっては、
∑_k (－k²+6k－4) を計算して、S_n を n の式で表すことが効果を発揮するときもあります。

こういったシグマ計算の練習も大切になるので、数列単元の学習において必要な計算力となります。

その一方で、楽で正確に答えを短時間で求めるという練習も意識しておくと、マーク型の試験のような時間制限が厳しい状況へのトレーニングとなるかと思います。

数列から定まる関数のグラフを描くことで、内容を可視化するということが役に立ちました。

この考え方も押さえるべき数列についての内容となります。

等差数列は一次関数という記事でも、数列を関数として捉え、グラフについての考察を述べています。

それでは、これで今回の記事を終了します。

読んで頂き、ありがとうございました。