一次不定方程式 ax+by=c の整数解【環論への布石】

一次不定方程式 ax+by=c の整数解について、特殊解と一般解の説明から始めます。
そして、図形と方程式の観点からベクトル方程式を用いて可視化します。
その後で、大学の環論入門の単項イデアル整域という背景を明らかにしています。
旧課程の高校の整数分野で具体的に慣れつつ、大学の数学へとつながれば幸いです。
大学の数学の内容は抽象的なので、高校の数学で地ならしをしてから、環論の内容へと踏み込みます。
高校生の方も、高校の発展内容として、イデアルを知るということで気分展開に最後に述べる単項イデアル整域の内容をご覧頂ければと思います。
一次不定方程式 :特殊解と一般解
【一次不定方程式】
a, b, c を整数とし、
方程式ax + by = c の整数解の組 (x, y) について考えます。
はじめに与えられた定数 a, b, c は整数です。そして、x と y に代入する数は整数に限定されているという状況です。
「ax + by = c」という方程式は、中学で習ったように、一次関数を定めます。
そして、x と y に整数しか代入できないということから、この関数の x の定義域は整数全体の部分集合となっています。
具体的に、a, b, c をそれぞれ 6, 8, 2 として、シンプルな一次関数を表す方程式で様子を見ることにします。
例えば、6x + 8y = 2
未知数 x と y が二個であるのに対して、方程式が一個しかない状況です。
x と y の組が存在したとしても、一通りとは限りません。
※ 線形代数学で学習する解の自由度1という状況です。
一般に、a, b, c にランダムに整数を当てはめた不定方程式だと整数解が一つも存在しないということが起こります。
しかし、6x + 8y = 2 については、整数解の組 (x, y) が存在します。しかも、無限通りの整数解が存在します。
中学で学習した一次関数のグラフと、ベクトル方程式を用いた図形と方程式の観点で、より詳しく説明します。
特殊解という座標から
6x + 8y = 2 の解を一つ、直観でも何でも良いので、一つ見つけます。
(x, y) = (3, -2) を代入すると、方程式の左辺と右辺の値がともに 2 となって等しいので、これは整数解の一つです。
このグラフ上の具体的な 1 点 (3, -2) を表している x = 3, y = -2 が特殊解です。
さらに、6x + 8y = 2 という直線グラフ上の点で、x 座標と y 座標の両方ともが整数となっている格子点をすべて見つけたいと考えます。
この x 座標と y 座標がどちらも整数になっている点を表すパラメータを使って一般的に表すものが一般解ということになります。
6x + 8y = 2 の一般解は、中学数学ですぐに分かります。
y = -3/4x + 1/4 ですから、
右に 4 進むと下に 3 進むという状況です。
この変化の割合が一定であることから、
特殊な点 (3, -2) から右に 4k 進み 下に 3k 進んだ点が直線上の格子点です。
※ ただし、パラメータ k には整数のみを代入することとします。
直線上の任意の点を P(x, y) とすると、
x = 3 + 4k, y = -2 - 3k
直線上の任意の点 P(x, y) の座標が、
(3 + 4k, -2-3k) と表されます。
k に具体的な整数を代入すると、具体的な直線上の格子点の座標が表示されます。
x = 3 + 4k, y = -2 - 3k という一般解が分かると、パラメータ k に具体的な整数を代入するだけで、直線上の格子点の座標を具体的に表示できるということになります。
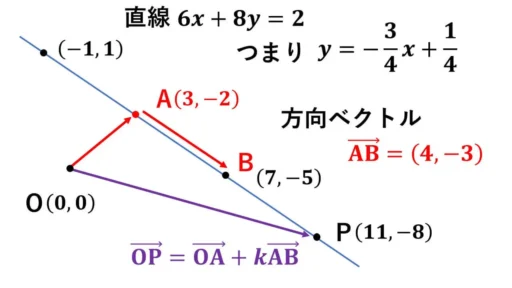
k = 2 のとき、上の図で P(11, -8) です。
ここまでが、文系数学用の考察です。ここから、理系の方向けに、ベクトルを用いて述べておきます。
変化の割合と方向
y = y = -3/4x + 1/4 という直線の傾きは一定で、右に 4 進むと下に 3 進むという方向です。
この方向ベクトルが (4, -3) です。
特殊解 x = 3, y = -2 から、
直線上の定点が A(3, -2) です。
特殊解から定まる定点を原点を中心とする位置ベクトルで表し、方向ベクトルで調整することで、直線上の任意の格子点 P を表すことができます。
ベクトル OA に方向ベクトル AB の k 倍を加えると、ベクトル OP となるということです。
式で x 成分と y 成分を表したものが、
x = 3 + 4k, y = -2 - 3k
k = 2 だと、ベクトル AB の長さの 2 倍分だけ右に動くので、P(11, -8) となっていたわけです。
一次不定方程式 :特殊解を求める
6x + 8y = 2 の一般解を求めるときに、先に特殊解を求めていました。
特殊解が分かれば、中学の数学で簡単に一般解をパラメータを一個使うことで表すことができます。
そのため、特殊解を求める方法が知りたいところです。
そこで、少し論理を使います。
はじめに与えらえた整数 a, b, c について、
ax + by = c の整数解の組 (x, y) が存在するということの必要条件を求めてみます。
※ ただし、a も b も 0 ではないとします。
互除法を用いることで、a と b の最大公約数 d が得られます。
a = dv, b = dw (v と w は整数)とすると、
c = ax + by = dsx + dty = d(vx +wy)
vx + wy は整数なので、c は d の倍数ということになります。
したがって、一次不定方程式の整数解が存在するときに、右辺の c は、a と b の最大公約数の倍数ということが分かりました。
では、実際に最大公約数を求めることから、特殊解を求めてみます。
実際に求める
8 = 1 × 6 + 2, 6 = 3 × 2 + 0
互除法から、6 と 8 の最大公約数が 2 と分かりました。
最大公約数を求めたときに出てきた等式たちを使って、右辺が 2 となる等式をつくります。
そのときに、6 に掛けられている整数と 8 に掛けられている整数が、整数解となります。
この例だと、はじめの等式から、
6 × (-1) + 8 × 1 = 2 とすぐに右辺が 2 となる等式が得られます。
x = -1, y = 1 と特殊解が得られました。
先ほどの x = 3, y = -2 とは違った特殊解が得られました。
この特殊解は、直線上の具体的な格子点を表すものなので、様々な格子点の座標が存在します。
(-1, 1) + k(4, -3) というベクトル方程式で直線上の格子点 P を表すこともできます。
見た目の式が違っても、直線上のすべての格子点を表すことができているので一般解です。
この例だと、互除法からすぐに特殊解が求まりましたが、計算が大変になることが多いです。
そこで、特殊解を求めるときに、合同式を使って特殊解を求める方法もあります。
※ 合同方程式の解き方という記事で、具体的な求め方について詳しく説明しています。
とにかく、特殊解から直線上の定点さえ求めれば、一次関数の変化の割合からすぐに一般解をパラメータを使って表すことができます。
それでは、これで今回のブログ記事を終了します。
読んで頂き、ありがとうございました。