素因数の個数 | 末尾に並ぶ0の個数を求めるアルゴリズムを解説

2023年10月30日

" 素因数の個数 “は、素因数分解をして掛け算だけの式にしたときに、その素因数の指数の数字のことです。

整数（自然数）についての問題で、末尾である一の位から 0 が何個続いて現れるかという問題が昔から有名です。

そこで、この手の問題に対するアルゴリズム（数学的な有限回の操作）を解説します。

まずは 10! という視覚的に捉えやすい状況で、仕組みを解説します。

10! を素因数分解したときに、2 の指数が何かを求めるところから解説をします。

素因数の個数 :10!の素因数2の指数

素因数分解は、素数たちの掛け算だけの式で表すということです。

12 = 2×2×3 と素数だけの掛け算の式で表したときを例に用語について述べておきます。

この 12 の素因数分解に現れている素数 2 と素数 3 を、12 の素因数といいます。

複数個の 2 が現れているので、指数を使って現れた回数が何回かを明確に示すことができます。

12 = 2²×3¹ です。

これで、12 を素因数分解したときに、素因数 2 は 2 個だけ現れ、素因数 3 は 1 個だけ現れるということが分かります。

この要領で、10!（10 の階乗）を素因数分解したときに、何個の素因数 2 が現れるのかを求めます。

つまり、10! を素因数分解したときの 2 の指数が何かということを求めるということです。

10×9×…×2×1 が 10 の階乗なので、10 個の自然数たちを全て素因数分解してから、それらを全て合わせるのは大変です。

しかし、論理と集合の考え方を使って、素因数 2 の指数を求めることができます。

では、10! を通じて仕組みを観察してみます。

素因数の個数を観察

1 以上 10 以下の範囲にある 2 の倍数を拾い上げます。

2, 4, 6, 8, 10 の 5 個です。

10! という掛け算を計算したときに、これら 5 個の 2 の倍数が現れます。

そのため、10! を素因数分解したときに、素因数 2 の個数は 5 以上ということが分かります。

ここで、2⁵ と早とちりをしないように注意です。

4 = 2² だから、4 の倍数からは素因数 2 が 2 個、出てきます。

8 = 2³ だから、8 の倍数からは素因数 2 が 3 個、出てきます。

視覚的に、何個の素因数 2 が登場しているのかを確認します。

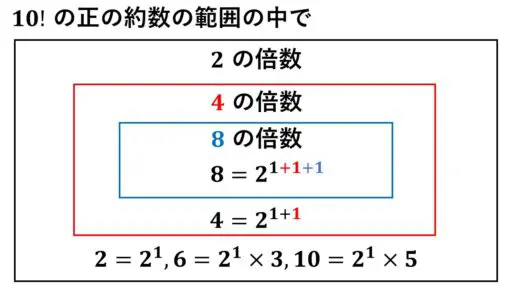
2, 4, 6, 8, 10 と 5 個の 2¹ の倍数の個数の分だけは、2 が素因数として現れます。

さらに 4 = 2² の倍数の個数の分だけ、つまり、4 と 8 のところから赤色で指数を書いている素因数 2 が現れます。

まだ続きます。

8 = 2³ の倍数の個数の分だけ、つまり、8 のところから青色で指数を書いている素因数 2 が現れます。

まとめると、次のようになります。

1 以上 10 以下の範囲にある 2¹ の倍数の個数は、5 個です。

同じく 2² の倍数の個数は、2 個です。

そして、2³ の倍数の個数は、1 個です。

ゆえに、(5+2+1) 個の素因数 2 が現れることになります。

つまり、2, 4, 6, 8, 10 のそれぞれから素因数 2 が 1 個ずつ現れ、さらに、4 と 8 から 1 個ずつ現れます。

そして、8 からは、もう 1 個。

これらを合計すると、
(5+2+1) 個、つまり、8 個の素因数 2 が現れることになります。

1 以上 10 以下の範囲にある 2¹ の倍数の個数と 2² の倍数の個数と 2³ の倍数の個数の和が、素因数 2 の個数となっているわけです。

これが、10! を素因数分解したときに、素因数 2 の指数を求める数学的な操作手順（アルゴリズム）になります。

この繰り返し操作で、順に何回の 2 が掛けられたのかを数えました。

終了の判断

2³ の倍数まで数えました。

しかし、2⁴ の倍数や 2⁵ の倍数は数えていません。

どうして、繰り返し処理を 2³ で止めたのかということも大切になります。

抽象的な数学の議論をしているときに、繰り返し処理が永遠に続くということも起こり得ます。

今回の考察では、繰り返し処理が 2³ の倍数が何個あるのかを数えるということで止まりました。

この繰り返し処理を終了する判断の根拠を述べておきます。

2¹, 2², 2³ は、10! に、最初から登場している自然数です。

そのため、素因数分解をしたときに、そこから素因数 2 が出現します。

それに対して、2⁴ は、10! に現れていません。

つまり、2⁴ は分解の対象外です。

これが 2³ の倍数を数えるというところで、止まる理由です。

素因数の個数 :末尾の0の個数

1750 だと、末尾に 0 が 1 個あります。

どうして末尾の 0 が 1 個だけなのかということは、素因数分解の形から分かります。

1750 = 2¹×5³×7 です。

素因数 2 と素因数 5 の個数が、末尾に並ぶ 0 の個数に関係します。

1750 という例だと、素因数 2 の指数よりも、素因数 5 の指数の方が大きくなっています。

そこで、
2¹×5³ = (2¹×5¹)×5²
= 10×5² = 5²×10¹

このように、式を書き換えることで、10 の指数だけ末尾から 0 が並ぶことが分かります。

1750 = 2¹×5³×7
= 7×5²×10¹

このように、素因数分解をしたときに、素因数 2 の指数と素因数 5 の指数の値が分かれば、末尾から 0 が何個並ぶのかを計算で求めることができます。

先ほどの 10! を例に、末尾の 0 の個数を計算してみます。

10!の末尾に並ぶ0の個数

先ほど求めたように、10! を素因数分解したときに、素因数 2 は 8 個だけ掛け算されていました。

つまり、2⁸ が 10! を素因数分解したときに現れます。

素因数 2 の個数を求めたときと同じ要領で、何回だけ素因数 5 が掛けられるのかを調べます。

5² > 10 なので、
10! には 5² は現れません。

そのため、5² は分解する対象ではありません。

このように、はじめにアルゴリズムが終了するのが、その素因数の何乗までかを押さえておくと気分が楽です。

1 以上 10 以下の自然数の範囲内で、5¹ の倍数は 5 と 10 の 2 個だけです。

よって、10! の素因子 5 は、
5¹ と 10 = 5¹×2 の 2 個だけが掛けられていることになります。

以上より、10! を素因数分解したときに、素因数 2 の指数は 8 で、素因数 5 の指数は 2 です。

2⁸×5² = 2⁶×(2²×5²)
= 2⁶×(2×5)²
= 2⁶×10² と指数計算を使って計算ができます。

これで、10! を素因数分解したときに、末尾に並ぶ 0 の個数が 2 個だと分かりました。

ここまでで、階乗を素因数分解したときに、何個の同じ素因数が掛けられているのかを求めるアルゴリズムを説明しました。

この数学的な有限回の操作を練習するために、全てを書き出すことが、より困難な状況を設定して説明します。

素因数の個数 :30!の末尾の0の個数

【練習問題】

30! を計算したとき、末尾に並ぶ 0 の個数を求めてください。

1 以上 30 以下の自然数を全て掛け合わせた値を手計算で求めることは困難です。

そこで、素因数分解をしたときの素因数 2 の指数と素因数 5 の指数を論理的に求めます。

階乗を素因数分解したときの素因数の指数を求める手順は、上で説明した通りです。

より求めやすい 5 の指数から求めます。

5² ≦ 30 < 5³ です。

30! のときは、30 以下となる最大の 5 の指数を先に押さえます。

5² は 30 以下ですが、5³ は 30 を超えてしまいます。

そのため、1 以上 30 以下の範囲に 5¹ の倍数と 5² の倍数が、それぞれ何個あるのかを求めます。

5×1, 5×2, 5×3,
5×4, 5×5, 5×6 の 6 個が範囲内にある 5¹ の倍数

5²×1 = 25 の 1 個のみが範囲内にある 5² の倍数です。

そのため、30! を素因数分解すると、素因数 5 の指数が計算できます。

6+1 = 7 より、
5⁷ が、30! を素因数分解したときの素因数 5 の部分です。

30! を計算するときに、奇数と偶数は交互に現れるので、素因数 5 よりも素因数 2 の方が出現する頻度が高いです。

そのため、計算をしなくても、素因数 2 の指数は 7 以上の自然数となっていることが分かります。

2⁷×5⁷ = (2×5)⁷ = 10⁷ だから、末尾に並ぶ 0 の個数は 7 個ということになります。

これで答えが求まりました。

30×29×…×2×1 を計算したときに、2 の倍数の方が出現する頻度が高いという直観で、2 の指数が 7 以上と踏んで答えを導きました。

念のために、素因数 2 の指数も求めておきます。

階乗の指数を求めるアルゴリズムの良い復習になるかと思います。

30!の素因数2の指数

2⁴ = 16 ≦ 30 < 32 = 2⁵ です。

まず最初の段階で、2⁴ までで範囲内の倍数の個数を求めるということを見切っておきます。

それでは、1 以上 30 以下の範囲にある 2¹ の倍数の個数を求めます。

2¹×1, … , 2¹×15 の 15 個が、該当する 2¹ の倍数の個数です。

今度は、2² の倍数の個数です。

2²×1, … , 2²×7 の 7 個が、該当する 2² の倍数の個数です。

順に 2³ の倍数の個数を求めます。

2³×1, … , 2³×3 の 3 個が、該当する 2³ の倍数の個数です。

ラストは、2⁴ の倍数の個数です。

2⁴×1 の 1 個が、該当する 2⁴ の倍数の個数です。

15+7+3+1 = 26 より、
2²⁶ が、30! を素因数分解したときの素因数 2 の部分です。

5⁷ と比べると、予想通り、素因数 2 の方が多く掛けられていることになります。

2²⁶×5⁷ から、10 の指数を求めると、末尾に並ぶ 0 の個数です。

やはり、
2⁷×5⁷ = (2×5)⁷ = 10⁷ ということになります。

今回は、整数分野について、階乗についての素因数分解で、掛けられる同じ素因数の個数を求める方法について解説をしました。

同じく 4の倍数の見分け方という高校数学の整数分野についての記事も投稿しています。

末尾に並ぶ 0 の個数について述べてきましたが、最後に一の位の数についても述べておきます。

一の位の数の求め方

例えば、3578 だと、
3578 = 357×10+8 です。

そのため、3578 を 10 で割ったときの余りが、一の位の数 8 となります。

このように、２桁以上の桁の自然数は、10 を用いて、一の位の数を分離することができます。

文字を用いた表し方は、証明問題で役に立つので、押さえておくと良いかと思います。

先ほどの 3578 だと、
a が 357 で、一の位の数 k が 8 です。

3578 = 357×10+8 ということを文字を使って一般化した表し方になります。

このことを使うと、次の命題が導けます。

一の位の数が等しい整数

【命題１】

整数 m と n を整数とする。

このとき、
「m と n の一の位の数が等しい」
ならば、「m－n は 10 の倍数」である。

＜証明＞

仮定より、m と n の一の位の数が等しいので、その数を k と置きます。

すると、ある整数 a と b を用いて、
m = 10a+k,
n = 10b+k と表すことができます。

よって、
m－n = 10(a－b) です。

a－b は整数なので、
m－n は 10 の倍数です。【証明完了】

この【命題２】は、一の位の数が等しい二つの整数で差をとった値の整数の一の位の数が 0 であるということを意味します。

整数が 10 の倍数ということは、一の位の数が 0 ということと同値になります。

文字で述べると複雑な感じがするので、具体例で観察をしてみます。

＜例＞

3578 と1438

どちらも一の位の数が 8 で等しくなっています。

3578 = 357×10+8,
1438 = 143×10+8 です。

差をとると、
3578－1438
= (357－143)×10

そのため、
3578－1438 の一の位の数は 0 となっています。

さらに論理を用いて、命題の逆も考えます。

逆もまた真

【命題２】

m と n を整数とする。

このとき、
「m－n が 10 の倍数」
ならば、「m と n の一の位の数は等しい」。

＜証明＞

m と n の一の位の数が異なると仮定します。

m の一の位の数を k, n の一の位の数を h と置きます。

ある整数 a と b を用いて、
m = 10a+k,
n = 10b+h と表せます。

今、k ≠ h なので、次の二つの場合が考えられます。

「k > h の場合」と「k < h の場合」です。

k > h の場合は、次のように矛盾が生じます。

m－n = 10(a－b)+(k－h)

k, h は 0 以上 9 以下の非負整数で、k が h よりも大きいという状況です。

そのため、0 < k－h < 10

m－n = 10(a－b)+(k－h) だから、
m－n を 10 で割ったときの余りが 1 より大きいということになります。

これは、m－n が 10 の倍数であるという仮定に矛盾します。

k < h の場合は、
n－m = 10(b－a)+(h－k) から矛盾が生じます。

先ほどと同様に、
0 < h－k < 10 です。

そのため、n－m を 10 で割ったときの余りが 1 よりも大きいということになります。

そのため、n－m は 10 で割り切れないということになります。

ところが、仮定から m－n が 10 の倍数です。

そのため、ある整数 t を用いて、
m－n = 10t と表すことができます。

すると、
n－m = －1×(m－n)
= 10×(－t) です。

これは、n－m が 10 の倍数ということです。

すなわち、n－m が 10 の倍数であり、10 の倍数でないということが起きています。

これは矛盾です。

以上より、背理法から、
m と n の一の位の数は等しいということになります。【証明完了】

【命題１】と【命題２】を厳密に証明しました。

一の位の数についての証明問題は、10 で割ったときの余りと検算の式を使って議論をするということが大切になります。

整数の内容は、一般的な文字を使って述べると難しい感じがするけれども、具体的に考えると命題が何を意味しているのか理解できるということが多いです。

厳密な証明は大学の数学の可換環論の内容に関わりますが、定理が意味することは証明が分からなくても納得できるという代表的なものがあります。

高校数学の整数分野から大学の数学へとつながる内容になります。

【より発展的な記事】

・7の倍数判定法
・フェルマーの小定理

それでは、これで記事を終了します。

読んで頂き、ありがとうございました。